氣泡,無處不在。
氣泡的宿命,就是破滅。
當我們看到可樂中的氣泡不斷往外冒時,當我們陪著小朋友吹著彩虹顏色的氣泡水時,我們可能并不知道:氣泡在火山爆發、玻璃制造、噴漆、化工設備腐蝕等等工業領域,氣泡的破裂是一個有趣而又極難處理的問題。
那么,問題來了:氣泡究竟是怎么破裂的呢?
在粘性液體中,氣泡會慢慢聚集在液體的表面。當氣泡浮出液面后,會形成一個球形帽狀的超薄液膜,氣體便置于其中。然后,液膜會形成一個越來越大的孔,被困其中的氣體得以逸出。沒有了氣體的支撐,液膜上的受力不平衡,氣泡周圍出現徑向褶皺,最終導致氣泡破裂。
先前的研究認為:由于薄膜的重量和開孔施加的幾何約束,形成褶皺,最終導致氣泡破裂。那么,薄膜上著這些褶皺是如何形成的?這些褶皺為什么會破裂呢?
最新研究表明:褶皺不穩定性既不依賴于重力,也不依賴于孔洞的存在。

薄片的起皺現象,存在于各種尺度范圍內,包括中性粒細胞吞噬作用、負責指紋的上皮組織發育和板塊構造的俯沖帶。一般而言,薄片起皺是因為當它們受到壓縮應力時,它們屈曲所需的能量比壓縮所需的能量少。
當一個薄的彈性薄板被拉伸、戳或包裹在彎曲的物體時,就會發生彎曲變形,從而形成褶皺。同樣,這也適用于粘性液體的彎曲。
在粘度為μ≈106 cP的硅油浴中,半徑為R=1 cm的坍塌氣泡產生的皺紋如圖1B所示。當氣泡高度Z達到距熔池表面約Z/R≈0.6時,皺紋出現在靠近氣泡邊緣的孤立環狀區域。在孔形成之前,氣泡在氣液界面上的平衡形狀是由氣泡內部的超額壓力ΔP與重力和毛細管力的組合之間的平衡建立的。由于本例中的氣泡半徑遠大于毛細管長度(γ/ρg)1/2≈1 mm,其中γ是表面張力,ρ是液體密度,g是重力引起的加速度,所以氣泡基本上延伸到浴缸表面之外并形成半球。重力驅使薄半球狀薄膜中的排水,導致氣泡壁向底部加厚。在表面張力和孔邊的局部曲率的驅動下,刺穿薄膜會產生一個孔,并促使薄膜從破裂點回縮。此外,刺穿薄膜會平衡界面上的壓力,導致ΔP→0。因此,孔洞的存在使作用在薄膜上的毛細和重力不平衡,最終導致氣泡破裂。考慮球帽上的表面單元dA,作用在膜厚h上的引力為Fg~ρhgdA,而向內拉膜的毛細管力為Fc~(4γ/R)dA(圖1A)。對于特征厚度為h≈10 μm的厘米大小的氣泡,毛細作用力(Fc)控制引力(Fg)的因子是Fc/Fg~4γ/(ρGRH)≈80。這種標度論證表明,塌陷過程是由表面張力主導的,而不是由重力主導的。
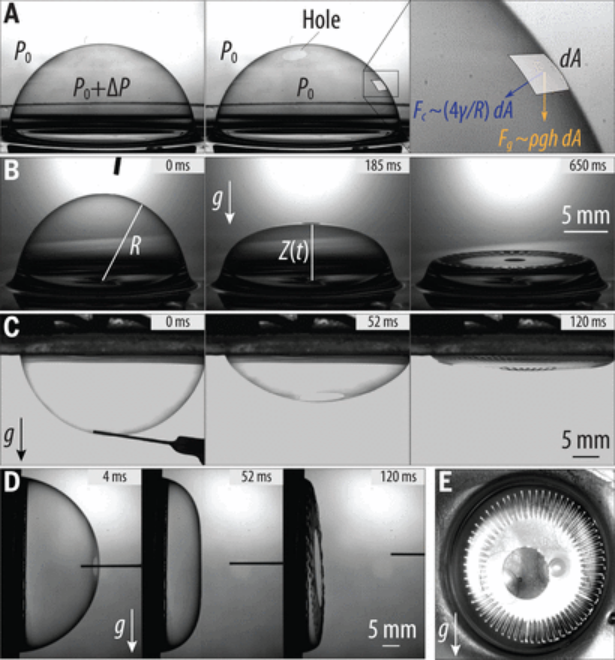
圖1. 粘性氣泡膜破裂時的崩塌。
為了驗證這一假設,研究人員在將氣泡顛倒后進行了一個相同的實驗(圖1C)。這種方法是可能的,因為液體具有足夠的粘性,可以在硅油流出倒置容器之前進行實驗。研究人員首先準備氣泡正面朝上,然后快速旋轉樣品,在幾秒鐘內使氣泡破裂。當反轉時,氣泡膜(厚度h≈2.4 μm)保持其形狀,并以~10 nm/s的速度在頂端增厚;因此,在旋轉或反轉過程中,膜的幾何形狀都沒有明顯的變化。如果重力和粘性是主導力量,那么倒置的氣泡就會向下伸長,正如之前的模擬所證明的那樣。相反,倒置的氣泡在重力的作用下向上收縮,在氣泡破裂的最后階段再次形成皺紋(圖1C)。運動的方向清楚地表明,重力不是導致坍塌的原因,但也不排除與褶皺有關的可能性。通過重復氣泡側面的實驗(圖1D),研究人員發現皺紋仍然出現(圖1E)。因此,研究人員得出結論,重力在氣泡破裂和褶皺失穩過程中起著微不足道的作用。
為了了解表面張力驅動氣泡崩塌的程度,研究人員測量了氣泡膜與熔池表面的最大距離Z(t)。從氣泡高度隨時間的演化,研究人員可以提取一個崩塌速度V=dZ/dt,它將決定崩塌的特征時間尺度。如果表面張力推動了崩塌,那么預計速度將取決于相互競爭的毛細和粘性力。實際上,平衡毛細管力γR和粘性力μh0V可得到特征速度V~γR/μh0,其中H0是頂點處的初始膜厚。因此,研究人員預計氣泡高度Z和相關的崩塌速度V的演變取決于薄膜的粘度和厚度。研究人員通過使用粘度為100、800和3000 Pa·s的硅油,并在破裂時改變薄膜厚度的系統實驗來驗證這一猜想。一旦被刺穿,氣泡破裂,當它到達浴缸表面時減速(圖2A)。從高速圖像中,研究人員通過在0.6<Z/R<1(23)范圍內平均下行速度dZ/dt來計算起皺開始時的代表速度V。增加硅油的粘度減緩了崩塌的速度。正如預期的那樣,當將歸一化高度Z/R與無量綱時間Vt/R作圖時,數據崩潰(圖2A,插圖)。
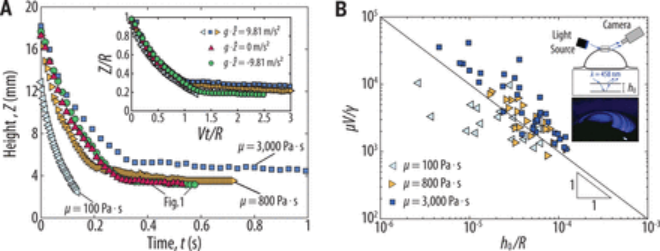
圖2. 氣泡膜厚度和粘度對塌縮動力學的影響。
為了獲得更深入的認識,研究人員結合光學技術和DebréGeas等人的引力排水理論,測定了氣泡頂端的破裂厚度H0。(17)。在單色光下,可以看到同心干涉條紋從氣泡的頂端發出(圖2B,插圖)。這些圓圈是軸對稱引流的證據,它們出現的速度可以用薄膜干涉法測量,以估計頂端的厚度。更薄的氣泡坍塌得更快(圖2B),正如從預測的比例V~γR/μh0(實線)所預期的那樣。研究人員承認實驗數據與這個簡單的定標有相當大的偏差,特別是對于100 Pa·s的硅油氣泡。然而,總體趨勢支持氣泡崩塌是由表面張力驅動的假設,在這種情況下,特征時間尺度R/V~μh0/γ變得與氣泡半徑無關。
Da Silveira等人的模型提出了重力和粘度導致起皺的原因:起皺的數量為n~(ρgRH3τc/μh2)1/2,其中RH為孔洞半徑,τc為薄膜崩塌所需的時間。孔的半徑在早期迅速增長,但在失穩過程中變慢到足以將其充分建模為常數。因此,這個模型聲稱褶皺的數量強烈依賴于孔的大小,當RH=0時沒有預測到褶皺。為了研究這個洞在皺紋形成中的作用,研究人員通過在放置硅油的培養皿底部鉆一個小口進行了實驗。研究人員將一條細管插入開口,注入空氣產生氣泡,然后用閥門密封開口。一旦氣泡到達表面,形成一個半球形的圓頂,研究人員就打開閥門,讓氣泡內的加壓空氣逸出。當空氣逸出時,ΔP→0,導致來自曲面的毛細管力不平衡,氣泡坍塌(圖3A)。在崩潰的最后階段,皺紋再次出現,這表明該孔只有通過消除氣泡表面的壓差才能起到褶皺的作用(圖3B)。因此,研究人員需要重新審視起皺動力學,從而為起皺機制推導出一致的物理圖像。
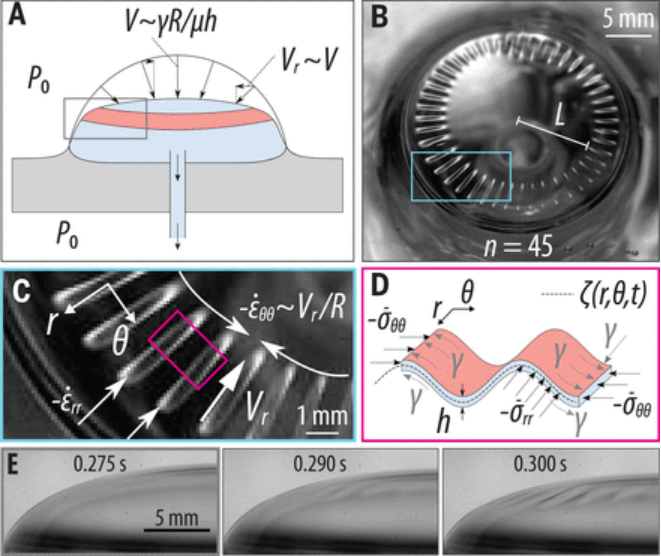
圖3. 氣泡崩塌而不破裂的機理。
研究人員提出了一種機制,當球形薄膜的破碎動力學導致環狀壓縮,克服了表面張力的平滑效應時,就會產生褶皺。在這里,毛細管驅動的坍塌在圓柱參照系中誘導出徑向速度,其尺度為Vr~V~γR/μh0(圖3A)。對于圖3C中定義的r,ε坐標系,徑向速度導致徑向壓縮率εrr,方位向壓縮率εθθ。對于牛頓流體,這種壓縮產生徑向應力σrr和環向應力σθθ,這可以與通過特勞頓模型的徑向壓縮速率相關,對于厚度為h的薄膜產生σrr~σθθ~4μhVr/R。從研究人員對虛擬現實的縮放可以得出,當忽略虛擬現實中的空間變化時,σrr~σθθ~γh/h0。因此,研究人員預計粉碎運動學將在外環(圖3A,紅環)產生比中心更大的壓應力,因為局部膜厚更大。不管這些壓應力的來源是什么,表面張力都會使液膜產生拉應力,從而使表面積最小化(圖3D)。研究人員認為,這些拉應力和壓應力的競爭導致了皺紋在距中心一段距離L處的位置(圖3B)。因為厚度剖面是未知的,所以不可能對應力場進行定量推導,因為預測皺紋的確切位置是必需的。如果表面張力超過整個薄板的壓應力,則薄板應保持光滑。然而,褶皺的存在表明,在離中心足夠遠的地方,壓應力占主導地位,以保持板材的光滑。當壓縮速度快于表面張力的平滑效應時,這種行為類似于一維粘性薄板的屈曲。為了避開厚度變化帶來的理論挑戰,研究人員將褶皺區域近似為一個恒定厚度h的環。
為了對皺紋的發展進行建模,研究人員推導了第一個F?ppl-von Kármán方程的動態版本,該方程描述了沿薄板中心線ζ(r,θ,t)的法向力平衡,如下所示(圖3D):
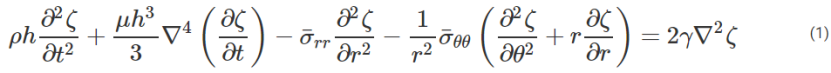
其中?4是雙調和算子,?2是拉普拉斯算子。由于觀察到多條徑向皺紋,研究人員尋求ζ(r,θ,t)=f(r)exp(ωt+inθ)形式的解。這里,f(r)確定褶皺幅度的徑向變化,ω是褶皺生長速率,n是褶皺數量。根據這些參數,公式1變為:
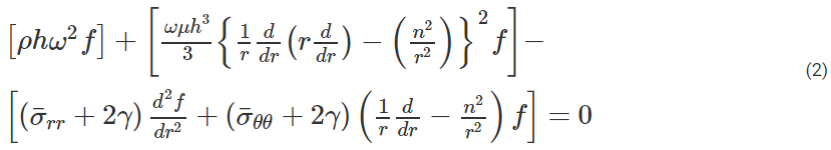
公式2中的三個方括號中的項分別對應于慣性、彎曲和壓縮。考慮到薄膜的高粘度,人們可能會忽略慣性效應。然而,皺紋發展的速度ω-1是~10 ms(圖3e),足夠短,慣性項變得不可忽略。事實上,對于一個典型的厚度h≈10 μm,研究人員發現慣性項和徑向壓縮項的比值為ρhR2ω2/γ~1,證明了在方程1中包含慣性是合理的。
在考慮軸對稱薄膜效應時,徑向應力σrr在褶皺發展過程中由于方位向應力σθθ的釋放而引起的褶皺有明顯的作用。當主導應力由方位向徑向變化時,方程2中的主導項對n的依賴關系也會發生變化。生長速率ω和褶皺數量n的比例關系可以從優勢平衡中獲得。具體地說,慣性項刻度為ρhω2,方位彎曲刻度為ωn4μh3/R4,徑向應力分量刻度為γ/R2。這三個主要項的同時平衡產生增長率ω?1~和褶皺數量n~(2γR2/ωμh3)1/4,或者等效:

為了測試Eq. 3中皺紋數量的比例,研究人員進行了系統的實驗,研究人員改變了氣泡的粘度和方向,同時將氣泡的尺寸限制在0.8 < R < 2 cm范圍內。研究人員還重復了有關疏散而不是穿透氣泡的實驗。研究人員利用崩塌時間R/V≡μh/γ來估計起皺膜厚度h,這樣得到的結果大約比頂點厚度h0大一個數量級(圖2C)。此外,研究人員還對更厚的結構進行了額外的實驗,從熔爐中提取吹出的熔融玻璃,并讓捕獲的空氣通過玻璃吹制管逸出。隨著漏氣,吹制的玻璃坍塌,呈褶皺狀,厚度為h≈200 μm (圖4A,插圖)。
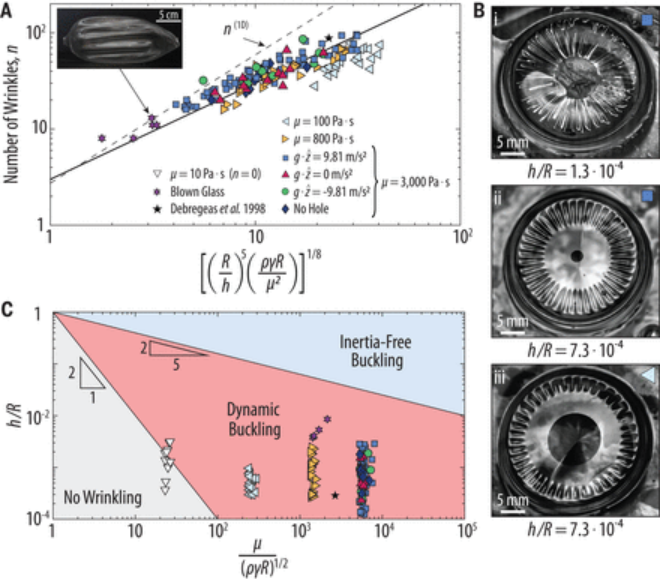
圖4. 數據和模型預測的比較。
皺紋數量的實驗結果如圖4A所示。根據初始半徑、厚度和粘度的不同,褶皺的數量可能在8到96之間。實驗結果(數據點)與研究人員從方程3得到的理論預測(實線)符合得很好。研究人員模型的局限性適用于薄膜最薄的數據。對于這些氣泡,坍塌是如此突然,以至于皺紋圖案失去了對稱性,皺紋橫跨整個氣泡(圖4Bi)。此外,考慮到圖2B中明顯的差異,在解釋100 Pa·s氣泡膜的數據時應該謹慎。這種差異可能部分源于厚度剖面的變化,這可能解釋了在這種較低粘度下觀察到的較大的孔尺寸和皺紋位置L(圖4,Bii和Biii)。請注意,研究人員的分析是基于這樣的假設,即褶皺位置L與氣泡半徑成正比,并且沒有考慮L與膜厚度或粘度的任何依賴關系。
研究人員的模型假設褶皺在球殼的軸對稱部分發展,這對于吹制的玻璃來說可能不太合適。具體地說,由于熔融的玻璃在加工成薄膜的過程中不斷旋轉,熔融的玻璃氣泡(圖4A,插圖)在崩潰前呈圓柱殼的形式,在崩潰后呈圓柱形,蓋子大致為半球形。對于這種情況,在求解公式2時,研究人員考慮了半徑為R的環,其中振幅f近似為常數。該方法得到了一維動態屈曲色散關系ρhω2+ωμh3n4/3R4-σθθn2/R2=0。線性穩定性分析表明,最不穩定的皺紋模式與生長速率ω(1D)~(γ2/ρμh4)1/3和皺紋數目n(1D)~[(R/h)5(ργR/μ2)]1/6有關,結果與Howell的結果相似。雖然用吹制玻璃進行的實驗數量不足以得出明確的結論,但研究人員預計一維縮放(圖4A,虛線)更適合于這個近乎圓柱形的幾何圖形。方程3的二維圓盤標度。對于涉及球帽氣泡幾何體的所有數據,更具說服力。
研究人員模型的一個預測是,并不是在所有條件下都會出現起皺。在一維和二維尺度中,慣性在決定褶皺數量方面起著關鍵作用。事實上,在這兩種情況下,當n>1時,或等效地h/R<(μ/)-2/5時,慣性是相關的,這是研究人員所有數據都滿足的標準(圖4C)。對于一維模型,如果忽略慣性,得到的屈曲輪廓將等同于直梁的歐拉屈曲(23)。慣性似乎也是不穩定增長率ω的主導因素:研究人員沒有發現粘度影響增長率時間的證據,這與研究人員的模型是一致的。對于皺紋的發展,它們生長的時間尺度必須小于崩潰的時間尺度μh/γ。因此,研究人員預測當h/R<(μ/)-2時不會出現褶皺。為了檢驗這一假設,研究人員破裂了粘度為μ=10 Pa·s的硅油形成的氣泡(圖4C,白色三角形),確實發現它們不支持任何褶皺。
研究人員已經證明,表面張力而不是重力驅動粘性表面氣泡在破裂后破裂,同樣也是降落傘不穩定性的原因。毛細管驅動的坍塌啟動了由縮回薄膜的慣性、壓縮和粘性彎曲同時相互作用所規定的動態屈曲不穩定性。研究人員的結果表明,類似的褶皺很可能出現在相對較小的彎曲薄膜上,其中重力的影響完全可以忽略不計。控制褶皺數量的方程1是用于研究彈性板殼變形的彈性F?ppl-von Kármán方程的粘性對應。因此,研究人員的系統提供了一個例子,即粘性薄片在快速壓縮時表現出類似彈性的不穩定性。基于粘性和彈性在這兩個系統中所起的相似作用,研究人員可以預見將研究人員的模型擴展到包含粘彈性薄膜的系統,其中粘彈性效應、毛細效應和慣性效應都對動力學有貢獻。例如,潛在攜帶病原體的氣溶膠的呼出與呼吸道粘彈性流體襯里中的薄氣泡膜的破裂有關。研究人員的推論是,在粘性薄膜破裂和收縮時,僅表面張力就可能引起翹曲,這暗示了這些薄膜折疊和截留空氣的可能性,從而豐富了氣溶膠化過程。
參考文獻
A new wrinkle on liquid sheets: Turning the mechanism of viscous bubble collapse upside down. Science, 2020.
DOI: 10.1126/science.aba0593
https://science.sciencemag.org/content/369/6504/685











