王楓,加州大學伯克利分校物理系教授�,專注于超快納米光學研究�����。自2004年博士畢業(yè),以通訊作者在Science����、Nature及其子刊發(fā)表大量高水平成果��,在石墨烯為代表的二維材料光學領域��,長期引領國際研究潮流。今天�����,我們要介紹的是王楓課題組今日在Nature最新發(fā)表的研究成果����,是關于單層石墨烯等離激元研究。
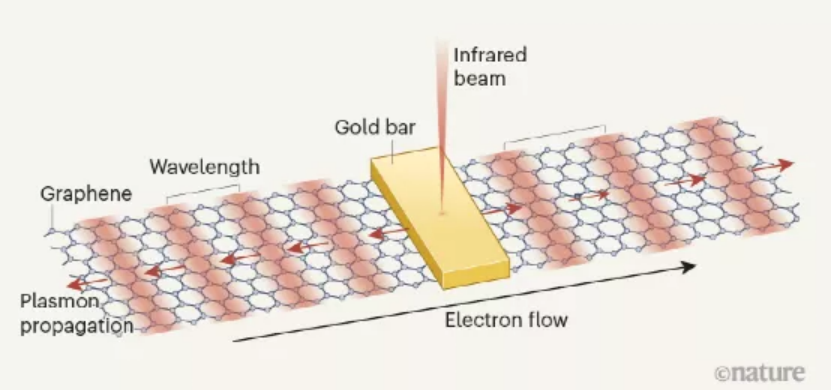
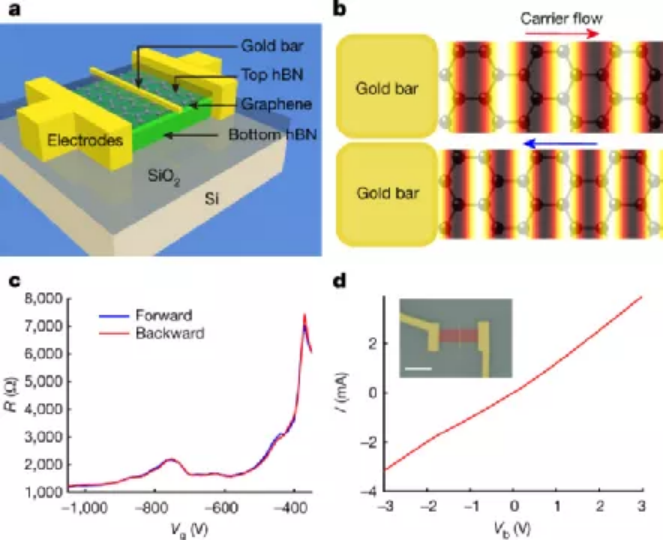
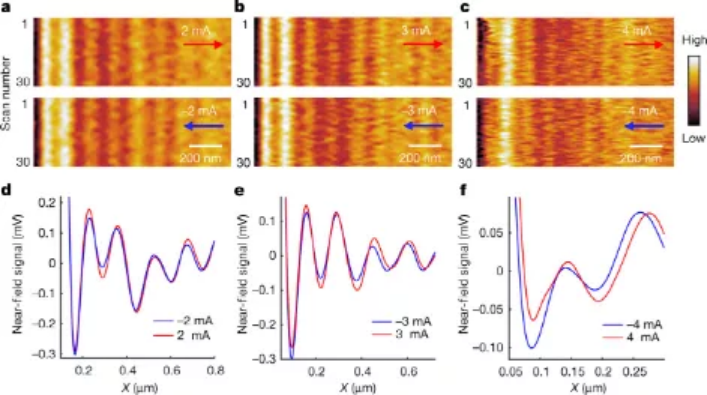
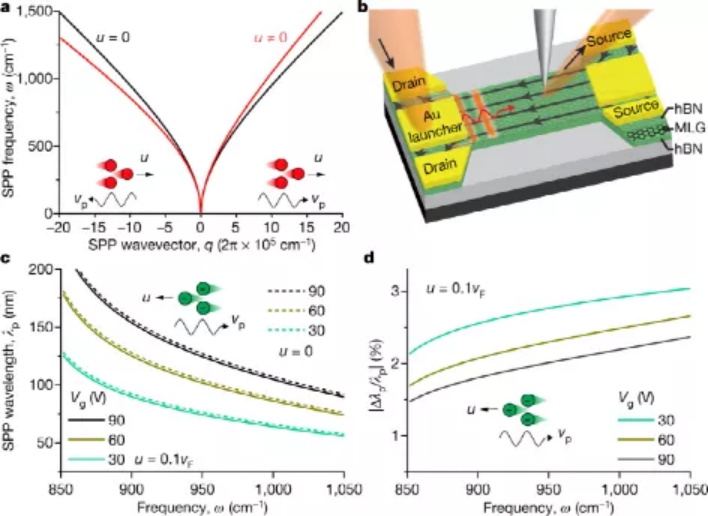
第一作者:Wenyu Zhao, Sihan Zhao通訊單位:加州大學伯克利分校�,勞倫斯伯克利國家實驗室通訊作者:D. N. Basov,D. A. Bandurin等離激元是光和集體電子振蕩的組合���。近日����,有研究表明在二維材料石墨烯中等離激元可以被漂移的電子拖拽����,這一研究可能極大促進光學物理學的發(fā)展�。如果波在與傳播方向垂直的方向振蕩,我們稱它為橫波���;如果波在與傳播方向平行的方向振蕩,我們稱它為縱波���。光是橫波,而等離子體是縱波。在Fizeau實驗中��,光和流動的水是不同的成分��,光可以在沒有介質(zhì)的情況下傳播���。然而��,對于一個等離子體而言,光和電子是不可分割的。因此�����,如果等離子體中的電子在電場中漂移��,那么等離子體就能被其組成的電子有效地拖動�。至關重要的是,因為等離激元的傳播速度比光慢得多,導致這種阻力效應比光通過移動介質(zhì)時更容易觀察到���。加州大學伯克利分校的Feng Wang教授的團隊和美國哥倫比亞大學D. N. Basov教授與麻省理工學院D. A. Bandurin教授的聯(lián)合團隊分別報道了石墨烯中等離子體被漂移電子拖動的現(xiàn)象。他們向金條發(fā)射了一束紅外光,從而在石墨烯中產(chǎn)生等離激元�����。隨后使用一種被稱為近場紅外納米鏡的成像方法直接可視化了低溫下的等離激元�。研究發(fā)現(xiàn),與石墨烯中的電子流方向相反的等離激元具有更短的波長。因此����,他們得出的結(jié)論是�,拖動效應使等離子體的波長改變了幾個百分點�。這種變化是顯著的�,因為它可以直接測量,而不需要借助敏感的光干涉技術(shù)。圖1石墨烯中等離子體被漂移電子拖動示意圖3���。1、因為石墨烯中的電子流動性高,且相對稀疏����。故而它們的漂移速度可以很大——比貴金屬大幾個數(shù)量級��。這一特性使得上述研究可以觀察到復雜的(非線性的)阻力效應。2��、石墨烯中的等離子體拖拽效應在愛因斯坦的狹義相對論中得到了很好的描述�,而在經(jīng)典物理學中卻沒有。對于傳統(tǒng)的二維電子氣體���,阻力效應滿足經(jīng)典關系,即等離子體的最終速度為其初始速度和電子漂移速度的總和�。然而��,對于石墨烯,需要狹義相對論來確定最終速度�����,上述研究都證明了這一點���。3���、石墨烯中的電子即使在室溫下也具有高度的流動性�,這表明在環(huán)境條件下,阻力效應可能是可以觀察到的��。對于傳統(tǒng)的二維電子氣體�,在研究這種效應之前需要低溫。圖3不同驅(qū)動電流下傳播等離激元的近場信號1。圖4石墨烯中等離子體菲索拖拽:理論和模型2���。1��、等離子體拖拽實驗為石墨烯中的電子-電子散射研究提供了新的思路��。阻力系數(shù)的測量量可以反映散射率�,如果這個速率(以能量為單位)比等離子體能量低�����,則阻力系數(shù)為0.25�。如果散射率相對于等離子體能量較高����,則阻力系數(shù)為0.5。因此�,等離子體拖拽效應提供了一種電子-電子散射率的測量方法�����,這對于分析涉及許多電子的相互作用特別有價值。2�����、漂移電子電流可以有效地打破時間反轉(zhuǎn)對稱性�����,這種效應可以很容易地應用于目標光子組件���,從而提高了器件的可控性和多功能能力����。阻力效應導致正向和反向傳播的等離激元具有不同的波長和速度�,從而引入了一種稱為非互易性的特性。結(jié)果����,時間反轉(zhuǎn)對稱性就被打破了����,如果時間方向被反轉(zhuǎn)�,系統(tǒng)的物理特性就會隨之改變。通常�,需要一個外部磁場或一個稱為手性泵浦的過程來打破這種對稱性�����。為了充分釋放石墨烯或其他等離子體系統(tǒng)中的這些非互易等離子體的潛力,還需要進行更進一步的實驗研究。1���、應該確定向前和向后移動的等離激元之間的傳播長度之差。理論工作表明,向前移動的等離激元比向后移動的等離激元的傳播長度要長得多��;而且在極端情況下����,向后移動的等離激元不能傳播。2、應該獲得更強的阻力效應�。需要獲得更強的阻力效應�����,就需要更高的漂移速度,這將導致嚴重的加熱問題——這個問題可以通過脈沖電流來緩解���。3、測量頻率范圍從遠紅外到中紅外的等離激元的阻力系數(shù)可以提供更完整的等離激元阻力效應的圖像����。4、近場紅外納米技術(shù)可以應用于傳統(tǒng)的二維電子氣體。系統(tǒng)比較傳統(tǒng)2D電子氣體和石墨烯的納米圖像將是十分必要的��,因為它能直接揭示阻力系數(shù)的差異�。1、Zhao, W., Zhao, S., Li, H. et al. Efficient Fizeau drag from Dirac electrons in monolayer graphene. Nature 594, 517–521 (2021).DOI:10.1038/s41586-021-03574-4https://doi.org/10.1038/s41586-021-03574-42、Dong, Y., Xiong, L., Phinney, I.Y. et al. Fizeau drag in graphene plasmonics. Nature 594, 513–516 (2021).DOI:10.1038/s41586-021-03640-xhttps://doi.org/10.1038/s41586-021-03640-x3、Hugen Yan. Nature 594, 498-499 (2021)DOI:10.1038/d41586-021-01599-3https://doi.org/10.1038/d41586-021-01599-3