特別說明:本文由學(xué)研匯技術(shù)中心原創(chuàng)撰寫,旨在分享相關(guān)科研知識(shí)。因?qū)W識(shí)有限,難免有所疏漏和錯(cuò)誤,請讀者批判性閱讀,也懇請大方之家批評(píng)指正。
原創(chuàng)丨彤心未泯(學(xué)研匯 技術(shù)中心)
編輯丨風(fēng)云

遠(yuǎn)離平衡態(tài)的量子多體系統(tǒng)存在著許多平衡態(tài)熱力學(xué)所不允許的各種奇異現(xiàn)象(如對(duì)稱性、拓?fù)洹⒕植炕椭芷谛则?qū)動(dòng))。理解和分類這些非常規(guī)階段是一個(gè)眾所周知的科學(xué)挑戰(zhàn)。雖然開創(chuàng)性的實(shí)驗(yàn)已經(jīng)觀察到了時(shí)間晶體相的特征,包括被困離子、固態(tài)自旋系統(tǒng)、超冷原子和超導(dǎo)量子位。然而,實(shí)現(xiàn)長壽命的Floquet SPT相(FSPT)階段需要拓?fù)洹⒍ㄎ缓椭芷谛则?qū)動(dòng)的微妙并發(fā),上述實(shí)驗(yàn)都沒有將拓?fù)渥鳛殛P(guān)鍵要素,因此理解非常規(guī)階段仍然是一個(gè)顯著的實(shí)驗(yàn)挑戰(zhàn)。
基于此,浙江大學(xué)王震研究員和清華大學(xué)鄧東靈助理教授等人報(bào)告了通過可編程超導(dǎo)量子比特陣列的數(shù)字量子模擬實(shí)現(xiàn)的一種獨(dú)特類型的非平衡狀態(tài)的物質(zhì)——Floquet對(duì)稱保護(hù)拓?fù)湎唷?/span>
作者使用深度超過 240并作用于26個(gè)量子位的電路,在多達(dá)40個(gè)驅(qū)動(dòng)周期內(nèi)觀察到邊緣自旋的穩(wěn)健的長壽命時(shí)間相關(guān)性和次諧波時(shí)間響應(yīng)。證明了亞諧波響應(yīng)與初始狀態(tài)無關(guān),并通過實(shí)驗(yàn)繪制出了Floquet對(duì)稱保護(hù)拓?fù)浜蜔嵯嘀g的相邊界。本工作的結(jié)果為探索奇異的非平衡相的物質(zhì)與當(dāng)前嘈雜的中等規(guī)模量子處理器建立了一個(gè)通用的數(shù)字模擬方法。
哈密頓量模型及其裝置
作者使用數(shù)字量子模擬,選擇合適的參數(shù),探究了FSPT階段時(shí)間平移對(duì)稱性對(duì)邊界處的破壞。使用神經(jīng)進(jìn)化算法來設(shè)計(jì)合適的量子電路,利用所得到的量子電路,在一個(gè)有26個(gè)量子位的倒裝芯片超導(dǎo)量子處理器上進(jìn)行了實(shí)驗(yàn)。
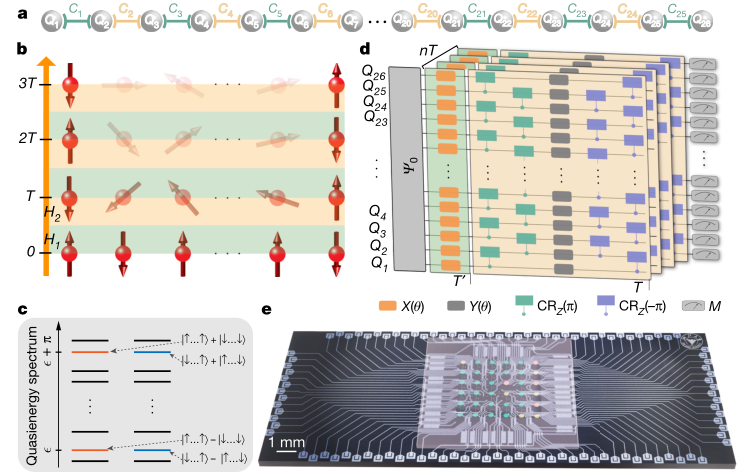
圖 FSPT階段和實(shí)驗(yàn)裝置的示意圖
邊緣對(duì)稱性破壞
通過邊界處局部磁化周期為2T的持續(xù)振蕩證明了FSPT 階段的特征是在鏈的邊界處打破離散的時(shí)間平移對(duì)稱性。作者繪制了不同相的無序平均局部磁化強(qiáng)度的時(shí)間演化,表明了邊界處時(shí)間平移對(duì)稱性的破壞而非整體上的破壞。
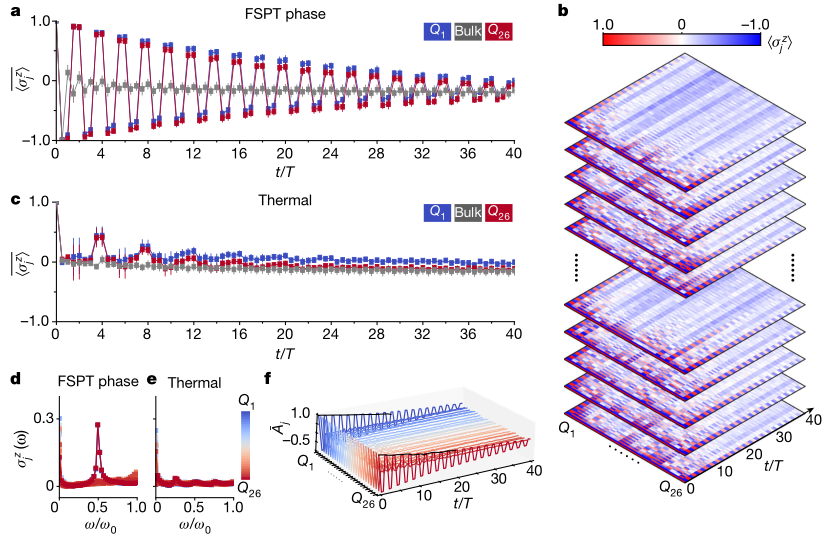
圖 使用26個(gè)可編程超導(dǎo)量子位觀察FSPT階段
局部化保護(hù)的拓?fù)錉顟B(tài)
為了建立FSPT階段,需要對(duì)其他初始狀態(tài)和其他局部可觀察量進(jìn)行額外的實(shí)驗(yàn)。作者展示了主體穩(wěn)定器不會(huì)破壞離散的時(shí)間平移對(duì)稱性,而是在它們的邊界處破壞。作者研究了糾纏光譜,證明了本征態(tài)的拓?fù)湫再|(zhì)。
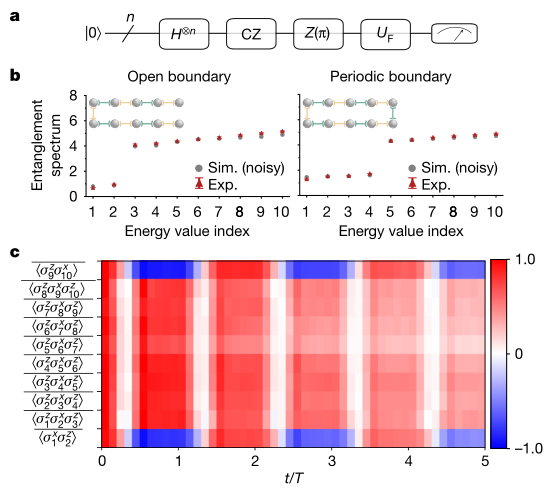
圖 具有隨機(jī)初始SPT狀態(tài)的穩(wěn)定器動(dòng)力學(xué)
相變
作者探究了FSPT相合其他熱相之間的相變,表明強(qiáng)相互作用會(huì)減少局部化并最終使系統(tǒng)熱化,在臨界出會(huì)出現(xiàn)兩相的過渡相。通過實(shí)驗(yàn)也證實(shí)了這種相變的存在并探測到轉(zhuǎn)變點(diǎn)。作者還使用本文的量子設(shè)備對(duì)其他模型進(jìn)行了數(shù)字模擬,證實(shí)了本文方法的普適性。
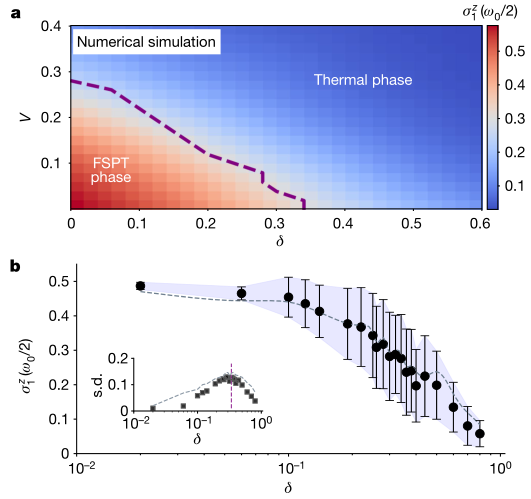
圖 相變的數(shù)值相圖和實(shí)驗(yàn)檢測
參考文獻(xiàn):
Xu Zhang, et al. Digital quantum simulation of Floquet symmetry-protected topological phases. Nature, 2022, 607:468-473.
DOI: 10.1038/s41586-022-04854-3.
https://www.nature.com/articles/s41586-022-04854-3











