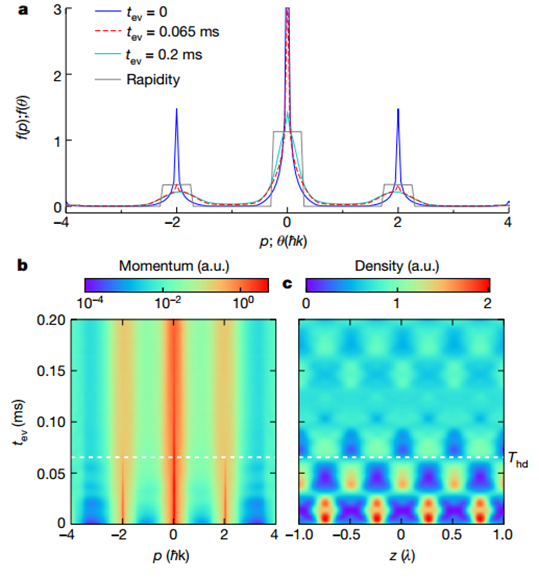
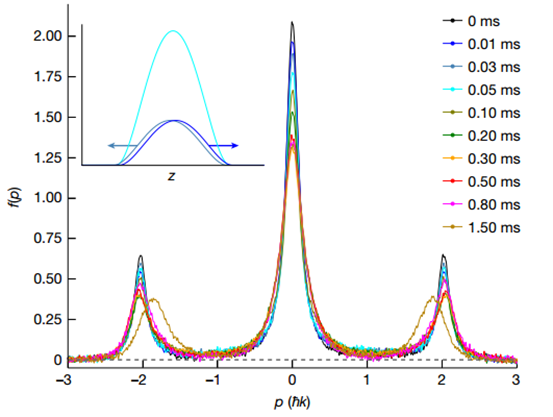
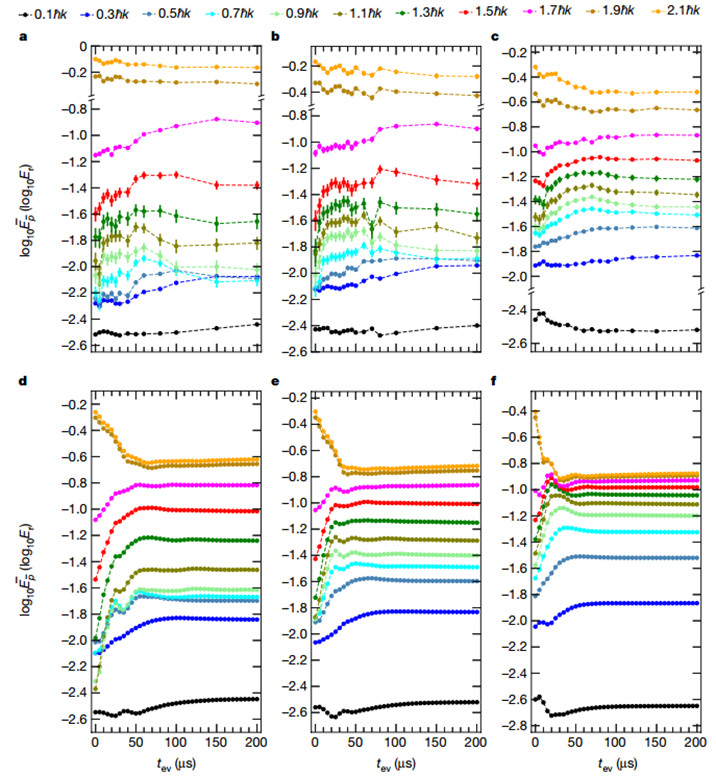
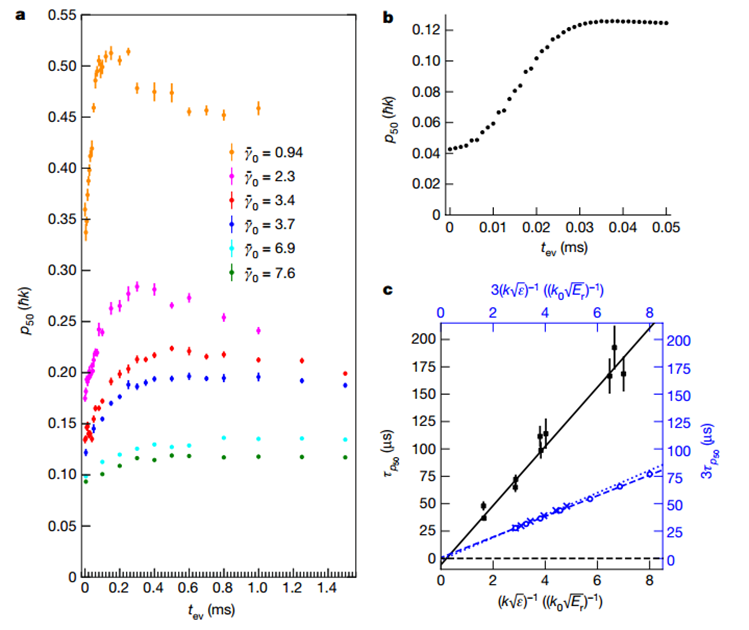
特別說明:本文由學研匯技術中心原創撰寫,旨在分享相關科研知識。因學識有限,難免有所疏漏和錯誤,請讀者批判性閱讀,也懇請大方之家批評指正。在局部熱平衡建立之前,流體動力學準確地描述了相對論重離子碰撞實驗。這種在最快的可用時間尺度上發生的流體動力學出人意料的快速發生被稱為流體動力學。當相互作用的量子系統以遠大于其基態能量密度的能量密度淬滅時,就會發生這種情況。在流體動力學過程中,能量會在非常不同的能量尺度上重新分配。流體動力學先于動量模式之間的局部平衡,后者是近可積系統中廣義吉布斯系綜的局部預熱化或不可積系統中的局部熱化。盡管許多量子動力學理論假設局部預熱化,但相關的時間尺度尚未通過實驗研究。有鑒于此,賓夕法尼亞州立大學David S. Weiss等人使用一系列一維 Bose 氣體來直接觀察流體動力化和局部預熱化。在應用布拉格散射脈沖后,流體動力化在遠距離動量模式之間的能量快速重新分配中很明顯,這發生在與布拉格峰值能量相關的時間尺度上。在附近動量模式之間的占用重新分配較慢中可以看到局部預熱化。作者發現系統中局部預熱化的時間尺度與所涉及的動量成反比。在流體動力化和局部預熱化過程中,現有理論無法對實驗進行定量建模。Tonks–Girardeau 極限中的精確理論計算顯示出定性相似的特征。1)Tonks-Girardeau (TG)氣體的流體動力學和局部預熱化的物理學作者使用捕獲的一維(1D)Bose 氣體和點接觸相互作用(Lieb-Lininger (LL)gas)觀察流體動力學,并用布拉格脈沖淬火。與超冷氣體的基態能量密度相比,脈沖賦予的高能量密度使得作者能夠認識到這種普遍現象。捕獲的LL氣體的近可積性提供了一個框架,可以從中繪制適用于不可積系統的一般圖景。由于1D Bose 氣體的強耦合TG極限是完全可解的,作者詳細解釋了均質TG氣體的流體動力學和局部預熱化的物理學。實驗從一束幾乎零溫度的一維氣體開始,該氣體由限制在藍色失諧2D晶格中的 87Rb 原子組成,并由交叉的紅色失諧偶極子俘獲光束提供軸向俘獲。作者在波矢k0 = 2π/(775 nm)的軸向晶格光束上脈沖6μs,然后測量動量分布作為脈沖后時間tev的函數,演示了不斷發展的動量分布。流體動力化導致系統能量分布的快速變化。為了可視化這種變化,作者對連續動量范圍內的動能進行積分,并將這些積分能量繪制為以反沖能量為單位的時間函數。正如預期的那樣,速度分布不會在這些時間尺度上演變。TG-氣體理論的各種流體動力學特征與相關實驗中的相似。在具有相同快度能量的情況下,理論中的局部預熱化速度是實驗中速度的兩倍以上。然而,由于曲線形狀的多樣性以及在此動量范圍內流體動力學和局部預熱時間尺度的適度分離,很難一致地提取局部預熱時間常數。為了更好地研究局部預熱化,關注動量模式之間的重新分配,這些模式的占用很大并且隨動量迅速變化。作者在動量分界線pf中發現了一個強大的可觀察到的,在中心峰中較低動量原子的f %和其余部分之間。通過找到p50處于其初始值和峰值之間一半的時間,從每條曲線中提取τp50。發現局部預熱化p50的中點,p50m,與成正比。Le, Y., Zhang, Y., Gopalakrishnan, S.et al. Observation of hydrodynamization and local prethermalization in 1D Bose gases. Nature (2023).DOI:10.1038/s41586-023-05979-9https://doi.org/10.1038/s41586-023-05979-9