特別說明：本文由米測技術(shù)中心原創(chuàng)撰寫，旨在分享相關(guān)科研知識。因?qū)W識有限，難免有所疏漏和錯誤，請讀者批判性閱讀，也懇請大方之家批評指正。原創(chuàng)丨Andy（米測 技術(shù)中心）
研究背景
隨著工程材料設(shè)計的發(fā)展，材料剛度和韌度之間的矛盾成為工程領(lǐng)域中一個根本性的問題。剛度是材料抵抗外力作用下變形的能力，而韌度是材料抵抗裂紋形成的能力。在結(jié)構(gòu)應(yīng)用中，材料必須抵抗不可逆的變形，并在外部加載下防止災(zāi)難性的破壞。然而，剛度和韌度通常是相互排斥的，因為具有韌性的材料必須足夠延展以容忍長裂紋，并在斷裂之前吸收更多的能量。為了解決這一矛盾，科學家們開始關(guān)注微結(jié)構(gòu)復(fù)合材料，并試圖找到既剛又韌的設(shè)計。微結(jié)構(gòu)復(fù)合材料是由兩種或多種基本材料構(gòu)成的，通過精心設(shè)計的微觀結(jié)構(gòu)來實現(xiàn)優(yōu)越的性能。然而，現(xiàn)有的設(shè)計方法存在一些問題。首先，由于模擬與實際之間的差異以及數(shù)據(jù)收集的低效性，尚未實現(xiàn)對具有最佳剛度-韌度折衷的微結(jié)構(gòu)復(fù)合材料的系統(tǒng)發(fā)現(xiàn)。其次，剛度和韌度的矛盾性質(zhì)要求設(shè)計不是單一的最佳解決方案，而是一組帕累托最優(yōu)解，使得找到整個帕累托前沿變得具有挑戰(zhàn)性。為了解決上述問題，近日，麻省理工學院計算機科學與人工智能實驗室， Wojciech Matusik教授團隊在Science Advances期刊發(fā)表題為“Computational discovery of microstructured composites with optimal stiffness-toughness trade-offs”的研究論文。本研究結(jié)合物理實驗、數(shù)值模擬和人工神經(jīng)網(wǎng)絡(luò)，他們設(shè)計了一個嵌套循環(huán)的工作流程，將力學測試器、基于有限元方法的模擬器和基于卷積神經(jīng)網(wǎng)絡(luò)的預(yù)測器整合在一起。這三個評估器分別具有不同的評估速度和準確性。通過在嵌套循環(huán)中相互協(xié)作，快速而不太準確的評估器提出微結(jié)構(gòu)設(shè)計，而更慢但更準確的評估器驗證這些設(shè)計，并用于改進快速評估器的準確性。通過該方法，研究團隊成功地克服了模擬與實際之間的差距，有效地發(fā)現(xiàn)了具有最佳剛度-韌度折衷的微結(jié)構(gòu)復(fù)合材料設(shè)計。該研究不僅填補了先前在這一領(lǐng)域的空白，而且提供了一個計算設(shè)計的藍圖，可在多個研究領(lǐng)域中應(yīng)用，如聚合物化學、流體動力學、氣象學和機器人技術(shù)。
研究內(nèi)容
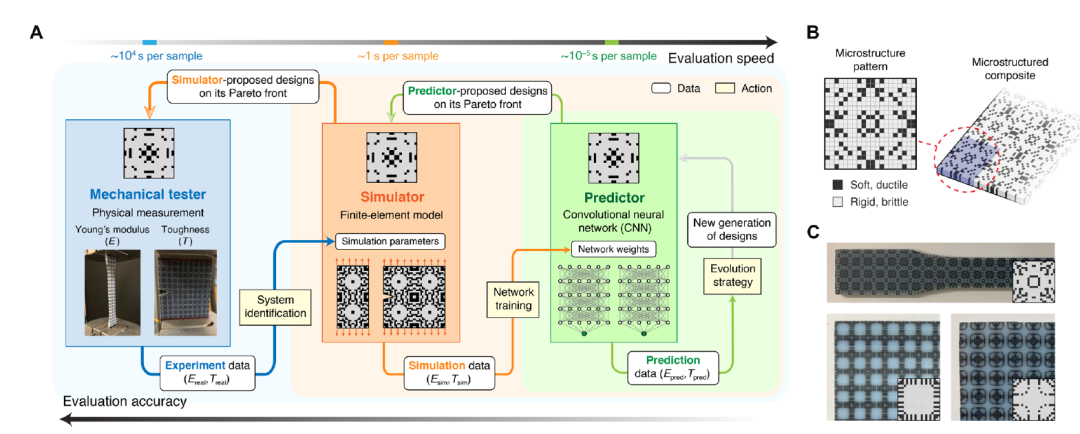
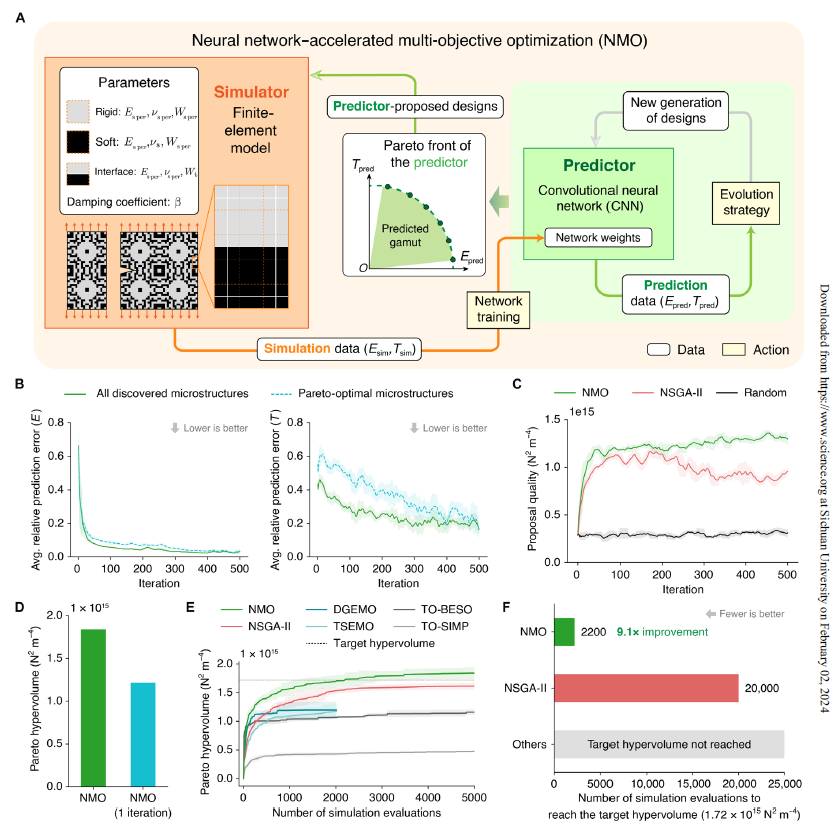
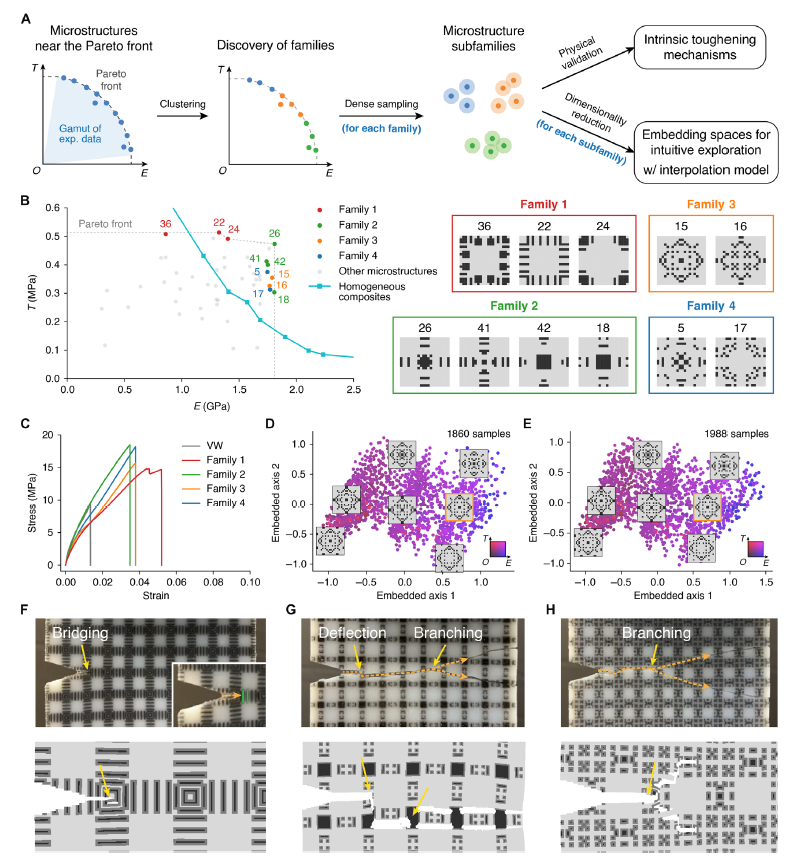
圖1展示了提出的嵌套循環(huán)工作流程，用于自動發(fā)現(xiàn)具有最佳剛度-韌度折衷的微結(jié)構(gòu)復(fù)合材料設(shè)計。該工作流程集成了機械測試儀、基于有限元方法（FEM）的模擬器和基于卷積神經(jīng)網(wǎng)絡(luò)（CNN）的預(yù)測器，它們在評估速度和準確性上存在差異。嵌套循環(huán)的全流程有效地提高了樣本效率，通過更快的評估器提出設(shè)計，然后由更準確的評估器驗證，并循環(huán)迭代以改進預(yù)測器的準確性。在圖1中（A）中顯示了提出的嵌套循環(huán)流程的工作流程。圖中箭頭指向相反方向表示了從更快評估器到更慢評估器的提議的帕累托最優(yōu)設(shè)計。在圖1（B）中展示了一個微結(jié)構(gòu)及其相應(yīng)的微結(jié)構(gòu)復(fù)合材料的示例。微結(jié)構(gòu)通過在二維網(wǎng)格上數(shù)字化排列兩種基本材料而定義，這些材料具有對比明顯的性質(zhì)。圖1（C）展示了制造的微結(jié)構(gòu)復(fù)合材料的樣本照片，標注了源微結(jié)構(gòu)模式。通過這一方法，研究者成功地解決了微結(jié)構(gòu)復(fù)合材料設(shè)計中剛度和韌度之間的折衷問題。 同時圖2突出了內(nèi)部循環(huán)中神經(jīng)網(wǎng)絡(luò)加速的多目標優(yōu)化（NMO）的關(guān)鍵結(jié)果。NMO利用卷積神經(jīng)網(wǎng)絡(luò)加速了模型訓練和設(shè)計提議的過程，通過迭代優(yōu)化找到模擬帕累托前沿上的微結(jié)構(gòu)設(shè)計，具有較高的設(shè)計提議質(zhì)量和更高的樣本效率，與其他多目標優(yōu)化算法相比表現(xiàn)更優(yōu)。這些結(jié)果提出了一種高效的計算方法，可用于解決工程材料設(shè)計中的剛度-韌度折衷問題，為微結(jié)構(gòu)復(fù)合材料設(shè)計和其他領(lǐng)域的計算設(shè)計提供了重要參考。 圖2. 擬議工作流程的內(nèi)循環(huán)，使用神經(jīng)網(wǎng)絡(luò)加速的多目標優(yōu)化（NMO）。圖3展示了提出的工作流程中的外部循環(huán)。該循環(huán)旨在通過不斷地將模擬器的輸出與實際測量結(jié)果進行匹配，縮小模擬與實際之間的差距，以找到經(jīng)過實驗證實的微結(jié)構(gòu)設(shè)計。在第0輪外部循環(huán)結(jié)束時（圖3A），選擇了八個從模擬帕累托前沿中發(fā)現(xiàn)的 帕累托最優(yōu)微結(jié)構(gòu)設(shè)計，接著作者制作樣本并進行了實際性能測試。然而，由于模擬器不包含復(fù)雜的材料模型或先進的斷裂力學，這些微結(jié)構(gòu)設(shè)計的模擬性能與其物理測量結(jié)果存在明顯差異。因此，外部循環(huán)通過系統(tǒng)識別來提高模擬器的準確性，從而盡可能地縮小模擬與實際之間的差距（圖3B）。作者對外部循環(huán)進行了四輪迭代，并在圖3C中展示了實驗數(shù)據(jù)和模擬范圍的演變情況。通過圖3D定量比較了它們的帕累托的進展。此外，在總共發(fā)現(xiàn)的50個微結(jié)構(gòu)中，作者選擇了6個設(shè)計作為最佳示例，并在圖3E中展示了它們的模式。隨著每一輪新增八個微結(jié)構(gòu)，模擬器的準確性隨時間增加，如圖3F所示。有了更高的準確性，模擬器能夠在每一輪中提出越來越好的微結(jié)構(gòu)設(shè)計，其性能由不斷提高的實驗的帕累托面積來表征（圖3G）。因此，即使使用相對簡單的模擬器，作者的流程也能夠同時彌合模擬與實際之間的差距，并找到具有經(jīng)過實驗證實的 帕累托最優(yōu)性能的微結(jié)構(gòu)。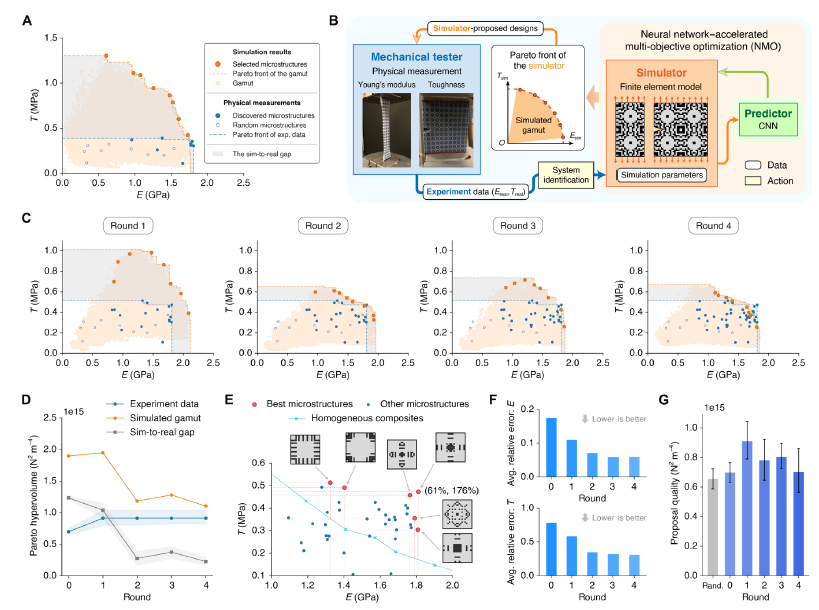 
圖4展示了通過對發(fā)現(xiàn)的帕累托最優(yōu)微結(jié)構(gòu)進行家族和內(nèi)在增韌機制分析的結(jié)果。首先作者設(shè)計了一個分析工作流程，將接近帕累托前沿的微結(jié)構(gòu)分為四個主要家族，并進一步劃分為子家族，以研究它們在低維嵌入空間中的模式變化（見圖4A）。每個家族的機械性能得到驗證，而每個子家族的模式變化則在嵌入空間中進行研究。圖4B展示了四個家族的種子微結(jié)構(gòu)及其與均質(zhì)復(fù)合材料相比的機械性能。圖4C呈現(xiàn)了每個家族中微結(jié)構(gòu)的代表性應(yīng)力-應(yīng)變曲線，展示了這些設(shè)計如何在維持可比楊氏模量的同時顯著提高抗斷裂性能，實現(xiàn)最佳的剛度-韌性權(quán)衡。此外，為了直觀地探索外觀和性能相似的微結(jié)構(gòu)，作者利用訓練有素的模擬器生成每個靠近實驗帕累托前沿的種子設(shè)計的本地范圍，并使用機器學習計算低維嵌入空間。最后，作者構(gòu)建了嵌入空間中鄰近模式的插值模型，以生成在密集采樣中可能被忽略的模式，從而最終完善了嵌入空間。通過分析測試標本和模擬視頻，作者成功地識別了增韌機制，例如橋接、偏轉(zhuǎn)和分支。這些機制抵抗裂紋擴展，并防止在均質(zhì)復(fù)合材料中觀察到的干凈劈裂的形成?？傊洸牧显赝ㄟ^裂紋鈍化提高韌性，而剛性材料元素保持整體連接以保持楊氏模量。作者的工作流程自動找到了平衡兩者之間的關(guān)鍵軟硬元素，而無需預(yù)先了解現(xiàn)有的增韌機制。這些結(jié)構(gòu)特征是通過完全計算方法生成的，而不是通過仿生學或試驗性的試錯法。 圖4. 使用發(fā)現(xiàn)的帕累托最優(yōu)微結(jié)構(gòu)進行家族和內(nèi)在增韌機制分析。
總結(jié)展望
本文采用了一種全新的、數(shù)據(jù)驅(qū)動的計算方法來解決復(fù)雜的材料設(shè)計問題。傳統(tǒng)上，材料設(shè)計通常依賴于手工設(shè)計或受生物啟發(fā)的方法，但這些方法通常受限于人類的知識和經(jīng)驗，并且往往無法全面地探索設(shè)計空間。相比之下，本文的方法利用了機器學習和優(yōu)化算法的強大能力，通過對大量模擬和實驗數(shù)據(jù)的分析，自動發(fā)現(xiàn)了最優(yōu)的微結(jié)構(gòu)設(shè)計，實現(xiàn)了優(yōu)越的性能表現(xiàn)。Beichen Li et al. ,Computational discovery of microstructured composites with optimal stiffness-toughness trade-offs.Sci. Adv.10,eadk4284(2024).DOI:10.1126/sciadv.adk4284。
