探測入射光的相位信息在光學成像與傳感領域有十分重要的應用價值,是制造全光場相機的重要基礎技術。傳統的解決方案一般采用微米級尺寸的透鏡系統或光柵檢測入射光的角度變化。然而由于入射光場的波動特性,這類系統在亞波長器件尺度上往往表現出非常有限的角度分辨能力,其較大的特征尺寸也給這類光電傳感器的片上集成制造帶來了困難。
近日,來自美國威斯康星大學和斯坦福大學的研究團隊在《Nature Nanotechnology》上報道了他們在這一技術領域的突破性進展。該研究團隊巧妙的利用了兩個共振腔發生相干耦合共振時光場的非對稱分布,成功地在亞波長器件尺度上實現了對入射光場的高精度角度探測(精度高達0.32度),為這一技術領域打開了全新的可能。

原文鏈接:https://www.nature.com/articles/s41565-018-0278-9
在這篇文章中,研究人員大量使用了基于FDTD的全電磁場數值模擬,直觀明了的介紹和演示了器件的工作原理,配合相關理論模型與實驗測試結果,對亞波長相干角度探測的物理機制和參數條件做出了充分和完備的論證。下面我們一起來了解一下。
我們知道空間上一對相互接近的共振腔,當他們之間的間距接近或小于模式波長時,會發生顯著的光學耦合(非厄米耦合),從而表現出所謂的超輻射(superradiance,即相位相張)與亞輻射(subradiance,即相位相消)集體共振效應。由于這兩種集體共振模式對入射波表現出不同的角度耦合特性,兩個共振腔中的光場將隨入射波角度的變化而形成不對稱的強度分布,從而反映出入射波的角度信息。在這篇文章中,研究人員利用了一組方形截面(約100 nm寬)的硅納米線波導作為相干共振腔,通過檢測左右納米線中受激光電流的大小比例來探測入射光波的角度,見圖1。
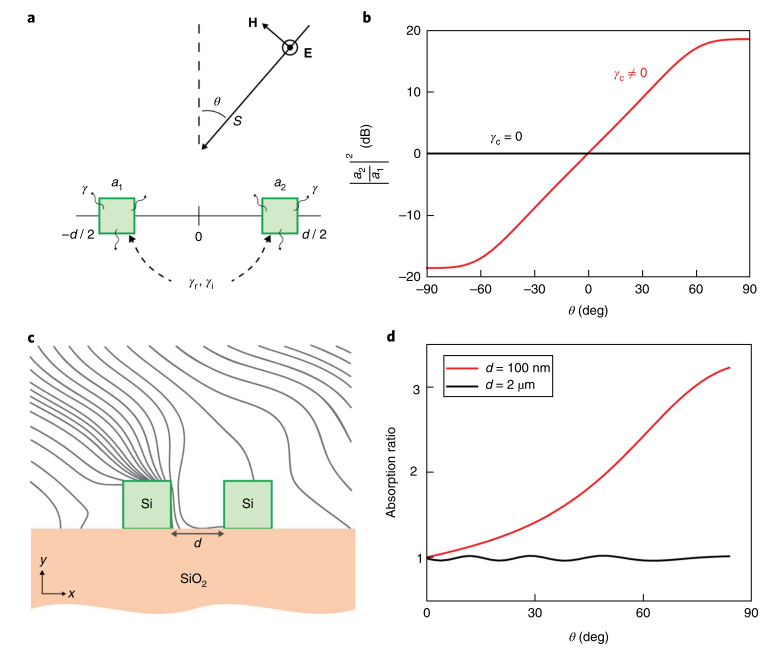
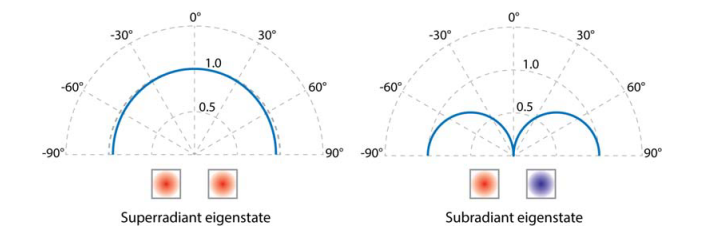
圖 1 a, 雙諧振器中的相干耦合模式理論示意圖。共振模式振幅為a1和a2,共振器相隔距離d。 S,γi和γr分別表示入射光功率,以及耦合強度的虛部和實部。γ為模式的衰減率。 H表示磁場,E表示電場; b,兩個諧振器中存儲能量的比率。在發生相干耦合時,這個比例很大程度上取決于激發光的入射角(紅線),而對于去耦合的諧振器,它保持為1(黑線)。以上兩種情況均使用d =0.05λ0, γ=0.01ω0。 γc= 9.8×10-3ω0當γc≠0。c,SiO 2襯底上的兩個Si納米線的橫截面圖,其中灰色曲線表示45°入射角的激發光Poynting流場線。 d,兩個Si納米線的吸收率比例隨入射角度的變化,其中d = 100 nm(紅色)和d =2μm(黑色)。在c,d中,入射波的電場沿z方向(TM偏振); e,耦合納米線中的超輻射(左)模式與亞輻射(右)模式及其角度耦合特性。兩共振腔的間距為模式波長的1/10,紅色與藍色相位相差?。
實驗表明,當納米線間距約為100 nm,入射波長為550 nm時,對于TM偏振的入射波,左右納米線的光電流的強度比例隨入射偏角在0度到70度之間的變化表現出近似線性的依賴關系;而對TE偏振的入射波,這一線性的依賴關系保持在最大入射角45度以內。因此,器件整體對± 45度范圍內的非極化光表現出良好的角度分辨能力。研究人員使用FDTD數值模擬,計算了硅納米線波導中的相關光學模式及其他們的近場吸收與遠場耦合特性,還原了在不同偏振類型的入射光下光電流隨入射角度的非對稱變化,與實驗結果形成較好的對應(見圖2,3)。
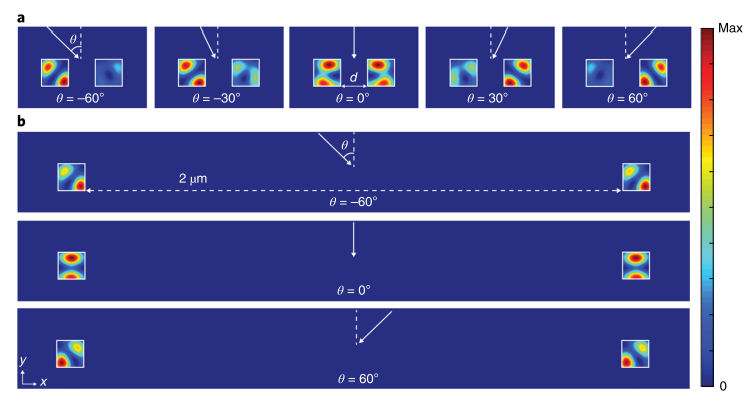
圖 2 a,納米線結構在不同入射角度下的光吸收率σ(ω)|E|2分布。 當d = 100nm時(有耦合),兩個納米線之間的吸收率對于不同入射角的變化清晰可見。b,當d =2μm時(無耦合),兩個納米線對于任何入射角都表現出幾乎相同的吸收分布。
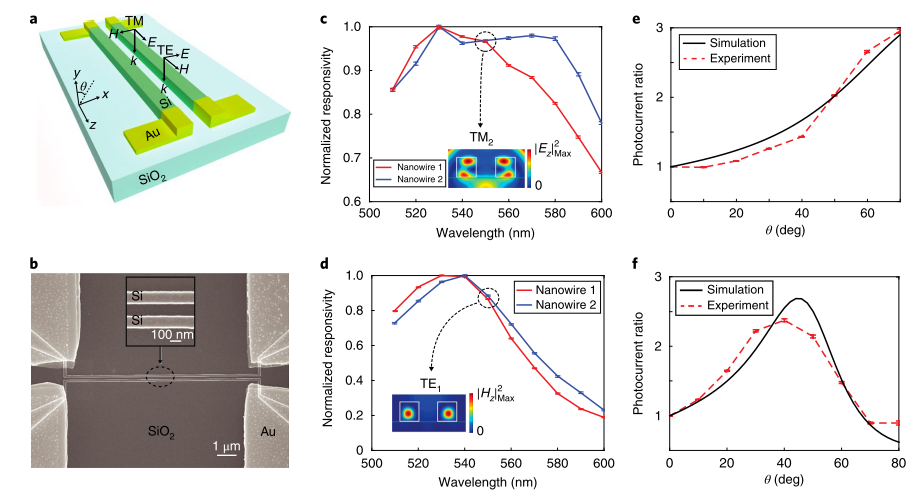
圖 3 a,采用兩根相干耦合Si納米線的角度檢測光電傳感器示意圖。綠色表示Si納米線,黃色表示Au電極。b,器件的SEM圖像。兩個Si線之間的間距約為105 nm。c,d,器件對TM(c)和TE(d)偏振光的歸一化響應譜。e,f,兩根納米線中光電流強度的比例對TM(e)和TE(f)偏振光隨入射角度的變化(黑線為FDTD模擬結果,紅線為試驗測試結果)。
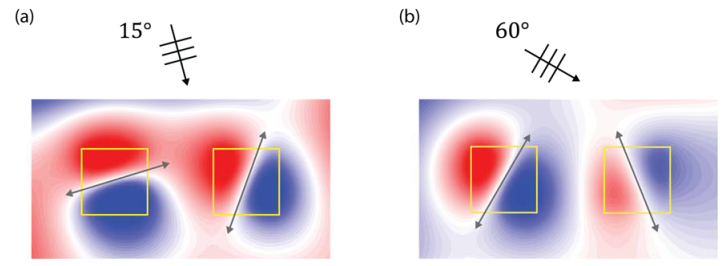
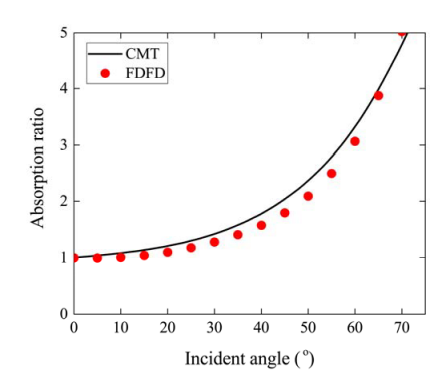
圖 4 a, b, 不帶襯底的簡化耦合納米線模型。納米線尺寸為100 nm×100 nm,間距也為100 nm。圖中為FDTD計算得出的波長為550 nm的TM偏正光在15°(a)和60°(b)入射角下納米線中的電場分布。c, 使用耦合模式理論(CMT)與FDTD全電磁波數值模擬分別得出的左右納米線吸收率比例的對比結果。
高級的研究成果中往往需要使用解析的理論模型對實驗現象給出更為嚴謹的理論說明,并進一步論證理論模型與實驗現象的異同之處。在這篇文章中,研究團隊使用了時域耦合模式理論(Temporal Coupled-Mode Theory)來描述耦合波導中的能量隨入射波偏角的變化,并且充分利用了高精度的FDTD全電磁場數值模擬,通過大量不失一般性的簡化模型還原了理論模型的推導結果,驗證了理論模型的正確性,從而建立了“理論模型——數值模擬——實驗結果”相互印證的完備論證(見圖4)。
在文章的最后,研究團隊利用了一個簡單的三角測距實驗展示了他們的納米線器件在實際情況下的工作性能。實驗表明,使用相干耦合納米線的角度傳感器可實現從數厘米到10米范圍內的精準測距,測距精度誤差在4 mm以內;相干納米線的角度探測誤差約為0.32度。這一測試結果也得到了FDTD數值模擬的支持。
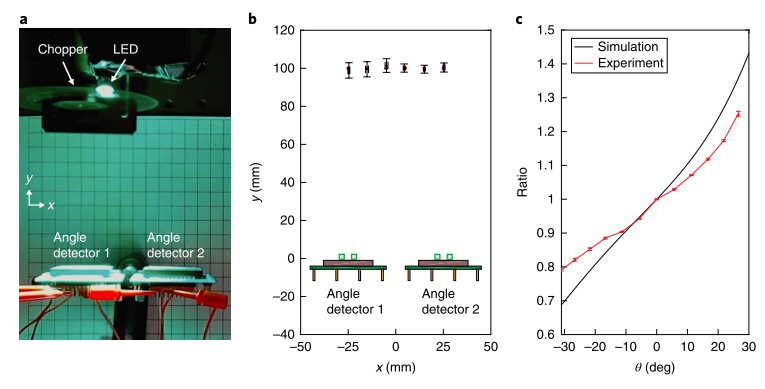
圖 5 a,三角測距實驗裝置。安裝在兩個獨立芯片上的兩個角度傳感探測器,在x方向上彼此相距50 mm。Y方向上100 mm處放置了嵌入直徑為5.6 mm的半球形玻璃透鏡中的LED光源。 b,在2D平面上進行的六次測量結果,紅點代表LED光源的真實位置。其中,對每個LED的位置進行了50次的重復測量生成誤差統計。c,采用FDTD全電磁場數值模擬和實驗測量的光電流比率的對比。其中,每個數據點進行了100次重復測量生成誤差統計。誤差線的平均長度為0.006。
總結一下,這篇來自威斯康星大學和斯坦福大學的《Nature Nanotechnology》采用了“理論模型——數值模擬——實驗結果”相互印證的研究方法,展示了一種新型的基于相干耦合納米線的亞波長角度檢測光電傳感器。該研究突破了傳統角度探測傳感器小型化和低精度的難題,為全光場傳感器的大規模片上集成提供了突破性的解決方案。文章中大量使用的FDTD全電磁數值模擬為整篇文章提供了強有力的論證支撐,成為連接理論模型與試驗觀測的利器。












