
在許多原子凝聚形成物質(zhì)的過程中,原子之間軌道雜化、原子之間形成化學(xué)鍵是兩個基本過程。人工原子能夠通過量子限域產(chǎn)生的離散能級,模擬真實過程的原子行為。因此人工原子能夠提供與固體非常類似的情況,模擬原子軌道雜化和原子之間形成化學(xué)鍵的過程。目前許多人工原子的研究能夠觀測發(fā)現(xiàn)原子之間形成化學(xué)鍵。但是,目前還沒有直接的實驗證據(jù)表征原子的軌道雜化。
有鑒于此,北京大學(xué)孫慶豐教授、北京師范大學(xué)何林教授、任雅寧等報道改變?nèi)斯ぴ拥男螤睿瑢崿F(xiàn)軌道雜化。束縛勢的各向異性特點導(dǎo)致人工原子之中具有不同軌道量子數(shù)的束縛態(tài)發(fā)生雜化。這項研究能夠在真實空間直接觀測雜化軌道,而且通過數(shù)值計算和推導(dǎo)重現(xiàn)了雜化軌道。
這項研究為無法通過真實原子的實驗構(gòu)筑人造物質(zhì)提供一種設(shè)計人工材料的新方法,此外,這項研究結(jié)果有助于漸進式控制(progressive control)各種體系的量子態(tài)。
天然原子vs人工原子
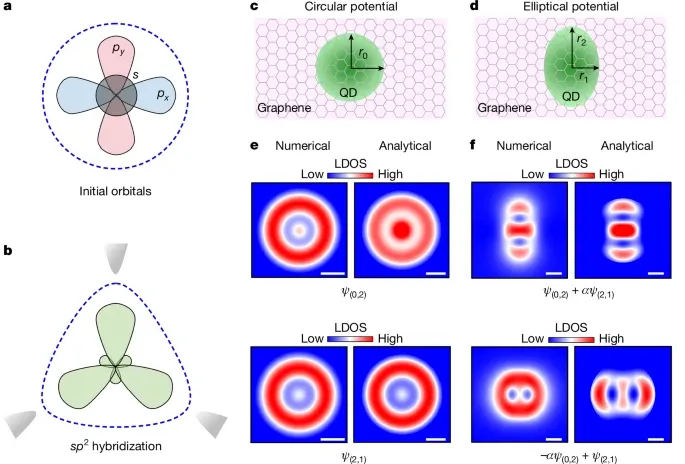
圖1. 天然原子、人工原子中的軌道雜化
對于單個真實原子,電子受到來自原子核的各向同性束縛勢。由于束縛勢的各向同性,形成了電子軌道,并由軌道量子數(shù)m來表征(圖1)。當許多原子相互聚集形成物質(zhì)之后,電子的各向同性電子勢受到相鄰原子的影響,因此不再表現(xiàn)為各向同性。
在石墨烯材料中,由于相鄰三個原子的影響,電子的等勢線形成三角形(圖1b),因此能量接近的s軌道、px軌道、py軌道發(fā)生雜化,形成疊加態(tài),這個現(xiàn)象是sp2雜化。
類似的,量子點(QD)也具有束縛勢,這種束縛勢同樣會導(dǎo)致電子出現(xiàn)離散的能級。作者研究圓形和橢圓形量子點,闡釋各向異性束縛勢對軌道雜化的影響(圖1c,d)。
其中,圓形量子點具有各向同性的束縛勢,這種各向同性束縛勢具有旋轉(zhuǎn)不變性的特點,因此能夠通過(m, n)表征束縛態(tài)能級(其中,m和n分別表示軌道量子數(shù)和主量子數(shù))。其中,(m, n)?=?(0, 1)和(1, 1)分別對應(yīng)于s1和p1軌道能級(能量最低的軌道、能量第二低的軌道),(m, n)?=?(0, 2)和(2, 1)對應(yīng)于s2和d1軌道能級。?(0, 2)和(2, 1)的局域態(tài)密度(LDOS)具有旋轉(zhuǎn)對稱性(圖1e),因此在原形QD中,這兩個態(tài)之間沒有發(fā)生雜化。
不同的是,對于橢圓形QD,旋轉(zhuǎn)對稱性被打破,因此,(0, 2)和(2, 1)的態(tài)能夠雜化,并且通過雜化產(chǎn)生新態(tài)。
![]()
ψsd+和ψsd?對于極角分別具有π周期性,其中形狀分別為θ形和旋轉(zhuǎn)后的θ形(圖1f)。
實驗測試
為了在實驗中研究各向異性束縛勢產(chǎn)生的軌道雜化,系統(tǒng)的研究各種不對稱勢下的石墨烯QD產(chǎn)生的準束縛態(tài)。如圖2a所示,將單層1T′ TMD(過渡金屬硫化物)納米島以插層方式引入石墨烯-2H晶相TMD的異質(zhì)結(jié)之中。
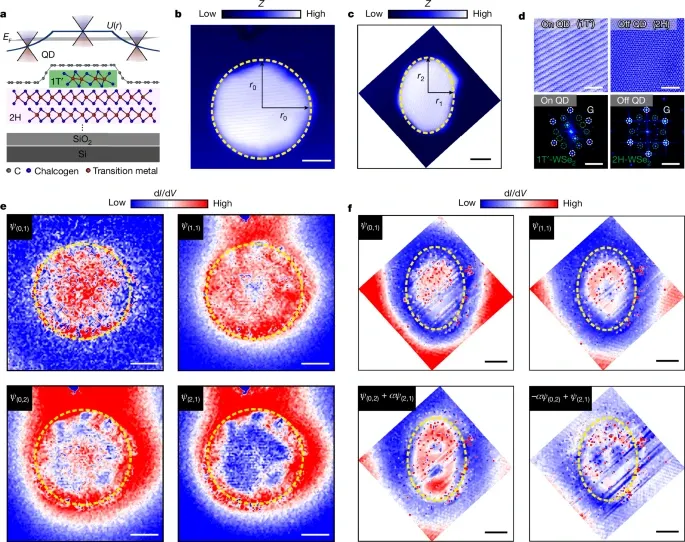
圖2. 實驗觀測雜化軌道
1T′晶相和2H晶相TMD對石墨烯層產(chǎn)生不同的電子摻雜,因此產(chǎn)生高品質(zhì)的p-n異質(zhì)結(jié),這種結(jié)構(gòu)是QDs。分別將單層石墨烯轉(zhuǎn)移到WSe2和MoSe2之上,結(jié)果表明兩個異質(zhì)結(jié)結(jié)構(gòu)非常類似。
如圖2b,c是石墨烯-WSe2異質(zhì)結(jié)得到的兩個QDs,分別為原形QD和橢圓形QD。原子分辨率的STM表征以及快速傅里葉變換成像(FFT)結(jié)果驗證界面WSe2島分別為1T′和2H(圖2d)。WSe2載體在擔(dān)載于之上的石墨烯形成確定的靜電勢,因此形成量子限域準束縛態(tài)。通過掃描隧道成像(STS)表征原形(圖2e)和橢圓形(圖2f)石墨烯量子點的束縛態(tài),能夠給出束縛態(tài)的局域態(tài)密度(LDOS)在實空間的調(diào)節(jié)情況。
如圖2c所示為橢圓形石墨烯量子點具有各向異性程度。發(fā)現(xiàn)雜化態(tài)呈現(xiàn)π周期性分布,并且通過數(shù)值計算和波函數(shù)解析得以驗證。因此,這個結(jié)果明確驗證了人工原子存在束縛勢的各向同性誘導(dǎo)產(chǎn)生sd雜化。
能級分裂
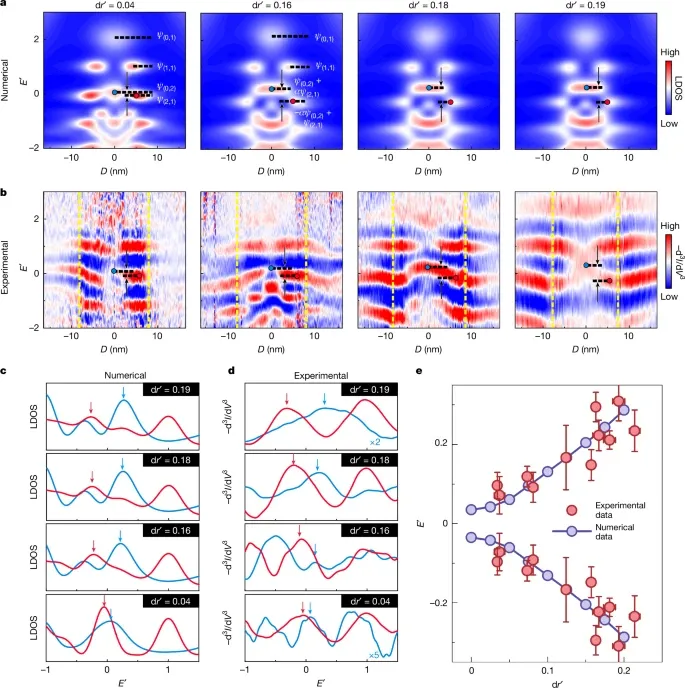
圖3. 雜化態(tài)的能級分裂vs各向異性度
s2 (0, 2)和d1 (2, 1)軌道雜化能夠通過s2, d1基組的effective Hamiltonian方程描述。當各向異性的程度增加,雜化增加,因此能量差增加,這種現(xiàn)象對應(yīng)于能量分裂形成雜化態(tài)sd+, sd?。通過數(shù)值計算LDOS的方法,分別計算各向異性增加的四個不同的石墨烯QDs的LDOS(圖3a)。圖3b給出實驗測試結(jié)果(空間-能量圖STS ?d3I/dV3,通過STM針尖調(diào)節(jié)各向異性的強度)。如圖3c,d所示,實驗測試和數(shù)值計算驗證能級分裂隨著dr′的增加的變化。準束縛態(tài)的能量和LDOS分布與圖2e,f和圖3b的結(jié)果接近。
此外,通過數(shù)值模擬計算圓形QD變?yōu)闄E圓形QD的過程。當保持各參數(shù)不變,dr′逐漸從0變?yōu)?.20(圖3a)。對每個dr′取值的情況下,分別得到準束縛態(tài)sd+和sd?的空間-能量圖和LDOS空間分布圖。并且,如圖3e所示,軌道雜化的能級分裂與實驗數(shù)據(jù)很好的符合。總之,這些研究結(jié)果通過實驗和數(shù)值模擬計算之間的相互支持,證實了各向異性導(dǎo)致軌道雜化以及能量分裂現(xiàn)象。
參考文獻
Mao, Y., Ren, HY., Zhou, XF. et al. Orbital hybridization in graphene-based artificial atoms. Nature (2025).
DOI:10.1038/s41586-025-08620-z
https://www.nature.com/articles/s41586-025-08620-z











