隨著仿真模擬技術的發展,仿真模擬技術被運用到了越來越多的科研鄰域之中。得益于仿真模擬的快速發展,計算模擬在電化學的運用日益廣泛,“實驗+計算模擬”的研究模式已逐漸形成。
以電化學方向為例,我們看看如何模擬循環伏安法和電化學阻抗譜。最近剛剛發表在Nature Communications ( Nature comm. 2019,10,1890.) 上的一篇文章就使用這兩種方法研究了硫化物型固體電解質材料。近年來,硫化物型固體電解質材料的研究引起了廣泛的關注在電池行業中。特別是磷的氧化分解和硫基固態電解質一直被認為是實現這一目標的主要障礙之實際的應用程序。
文章演示了這種現象在什么時候可以被利用硫代磷酸鋰被用作電化學上的“開關”功能氧化還原介質發生器的激活,商用散裝硫化鋰高達70瓦特%硫化鋰電極含量。x射線吸附近邊能譜與電化學阻抗譜和拉曼光譜表明了催化作用的產生硫化鋰第一次充電時的氧化還原介質。與預溶劑化氧化還原相反該設計將硫化鋰的活化過程從介質中分離出來預溶劑化氧化還原對電池低電解質含量運行的限制介質。在嚴格的測試條件下,證明了其合理的性能。
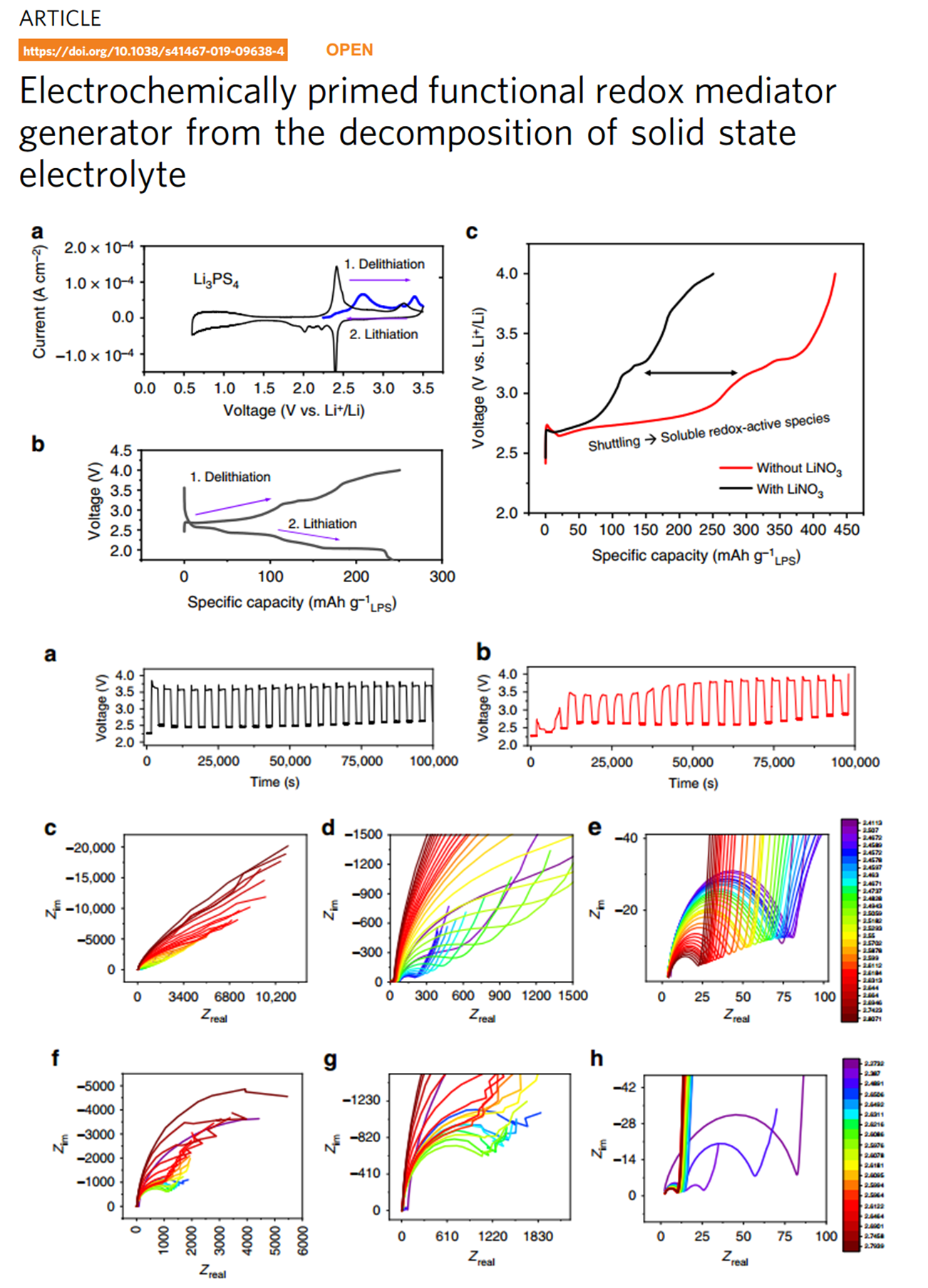
應用循環伏安法和電化學阻抗譜研究硫化物型固體電解質材料
在電化學領域,循環伏安法分析技術通常使用微盤作為工作電極。與宏觀電極不同,微型電極上的擴散在實驗中的時間尺度上發生得非常快。為了簡化分析,我們可以采用近似法,即假設微盤在伏安法研究的時間尺度上具有穩態擴散屬性,從而消除了對時變模型的需要。電化學阻抗譜是一種通用的實驗技術,可提供有關電化學電池的各種物理和化學現象的信息。通過對相關物理過程進行建模,我們可以建設性地解釋實驗結果,并評估控制電池的物理量的大小。
一、循環伏安法
1. 原理
循環伏安法是一種電化學技術。在該技術中,電位被反復掃描(例如,在起始電位和終止電位之間),同時測量產生的電流。伏安法一次掃描便可以提供關于系統行為的多樣性信息,如電極表面的吸附-解吸過程,從而使該方法廣泛應用于多種系統。
科研人員使用包括微盤電極在內的不同類型的電極作為循環伏安法的工作電極。微盤電極 是一種具有微米級半徑的盤形電極,嵌入與電極表面齊平的絕緣體中。由于尺寸較小,微盤電極擁有相對其尺寸而言較大的擴散層和較小的總電流,從而有助于實現穩態條件。電極尺寸越小,達到穩態所需的時間就越短。另外,微盤電極即使在很高的掃描速率下,失真度也很小。使用小尺寸電極研究伏安法的優勢在于它們具有使電流密度最大化的傳質特性,從而使科學家能夠觀察到在宏電極中無法觀察到的電化學行為。
在標準循環伏安實驗中,除了用來探測溶液的工作電極外,還包括配有對電極(用于形成完整電路)和參比電極(未極化)的電池,因此,假設其電位是恒定的,通過參比電極電位,可以測量工作電極或對電極的電位。另外,可加入支持電解質以增加溶液的電導率。
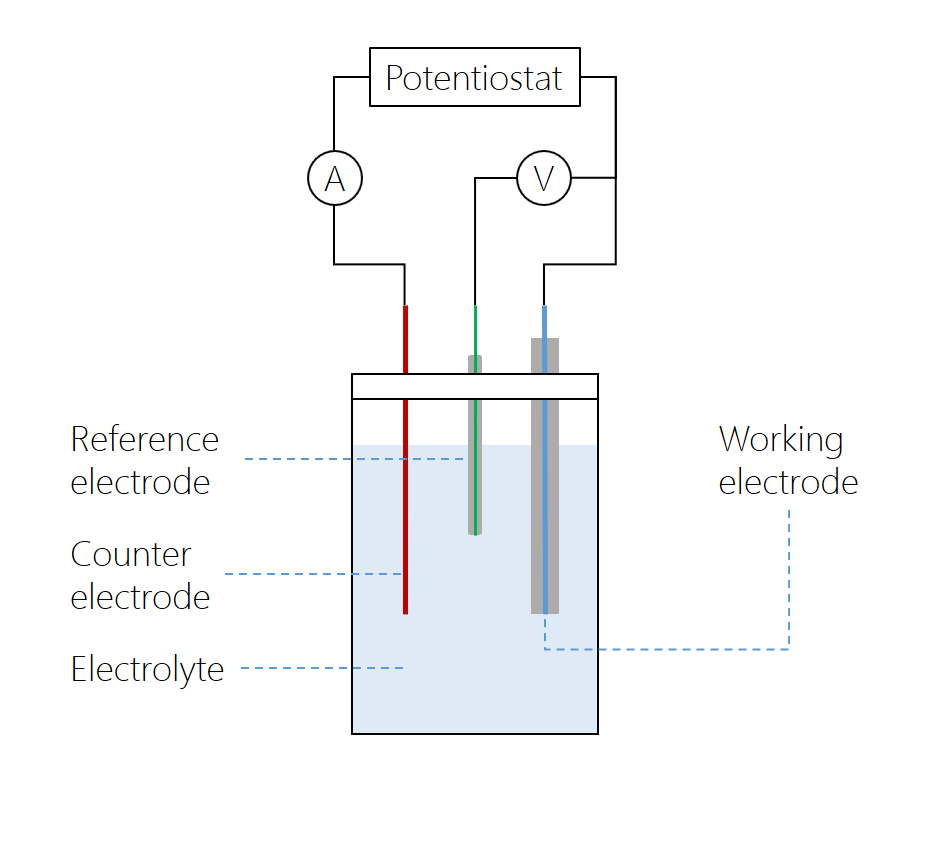
微盤電極是工作電極,對電極處于相對較遠的位置。參比電極通過高阻抗伏特計與工作電極連接,工作電極和對電極之間的電流通過低阻抗安培計測量。穩壓器通過電池調節電位。在現代穩壓器中,伏特計和安培計一般是內置的。
循環伏安系統由一個穩壓器、電流-電壓轉換器以及生成伏安圖的數據采集系統組成,其中穩壓器使工作電極電位相對于參比電極保持在恒定水平。循環伏安圖有多種不同的形狀,一般通過繪制電流密度與外加電位的關系圖表示。在使用平面電極測量單個可逆電極反應的情況下,圖形呈現“雙峰”形狀。然而,圖形的形狀取決于電極和電解質的組成。
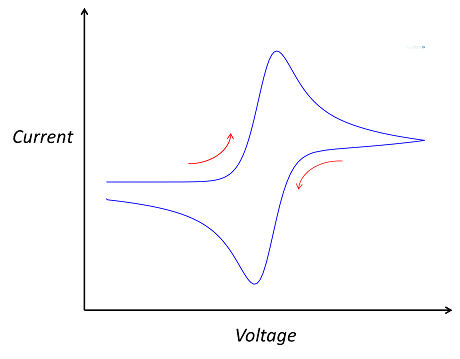
典型的循環伏安圖雙峰形狀
2. 通過 COMSOL Multiphysics 在微盤電極上建立伏安法模型
模型包含一個二維軸對稱域,COMSOL Multiphysics? 軟件的無限元 域特性用于將同心區域的本體溶液擴展到無窮大。因為我們假設電化學電池比電極大幾個數量級,所以這是一種合適的近似法。
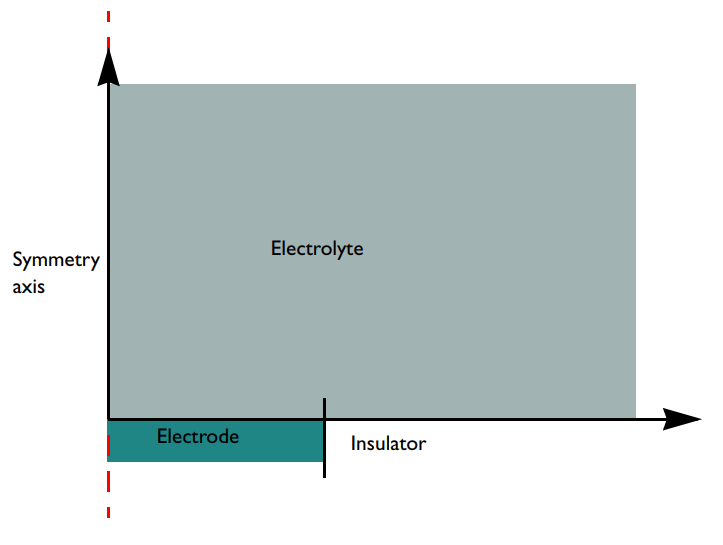
微盤電極與周圍電解質的幾何模型示意圖。注意,與第一幅圖中的電池相比,該圖結構是上下顛倒的,電極表面朝上,而第一幅圖顯示的電極表面朝下(實際結構中的規范)。模型中沒有考慮重力,所以在這種情況下,翻轉對模型結果沒有影響。
如上所述,我們添加支持電解質以提高電解質的電導率。由于加入了大量的支持電解質,可以假設電解質電位是一個常數,并設置 φl= 0。為了模擬這種情況下的電化學過程,我們使用了電分析 接口,該接口擁有這一假設條件下氧化還原電對的反應物和生成物的化學物質傳遞方程。擴散方程描述了電活性物質 A 和 B 在穩態條件下的化學傳遞。
接下來,我們將邊界應用到本體溶液,使表面、電極和物質絕緣,并解釋其中涉及的電化學過程。例如,物質 A 是電極邊界的反應物,當被氧化時,失去一個電子,形成產物 B。
在建立了邊界方程后,我們開始進行研究。在本例中,我們不需要進行時變分析,因為使用了近似法,即假設微型電極在時間尺度上具有穩態擴散屬性。穩態結果是準確的,這意味著我們可以使用穩態研究。在近似準靜態下,我們使用參數掃描來獲得伏安掃描電位處的電流密度。
3. 結果分析
下圖顯示了微盤電極周圍的穩態濃度分布剖面圖(注意二維截面的不同形狀)。在離電極較遠的地方,濃度呈半球形分布;但在靠近微盤邊緣處,通量增加。對于動力學較快的情況,電極表面的濃度是均勻的,導致電極表面的通量分布略有不均,這意味著反應分布也略有不均。
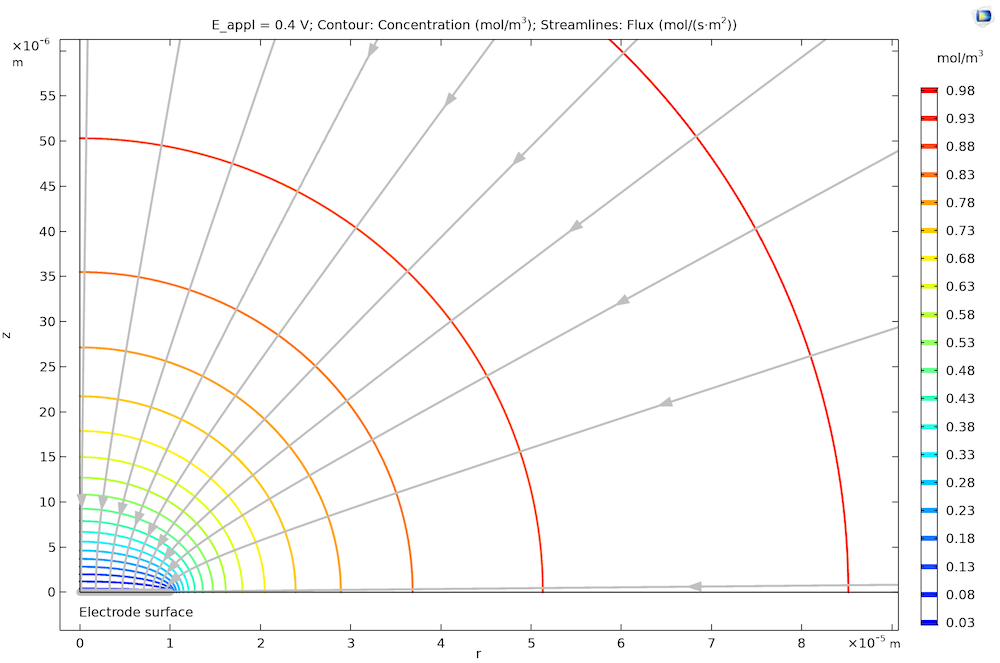
A 物質在微盤電極上傳遞控制的氧化反應濃度分布剖面圖。注意在 r = 0 處有旋轉對稱性。流線顯示微盤電極表面的通量(灰色突出顯示)以及反應速率,在邊緣地帶(右)比中心部位(左)要高。
接下來,我們來看看循環伏安圖,該圖顯示了電極動力學與擴散或化學物質傳遞之間的關系,其中電流密度是有限的。
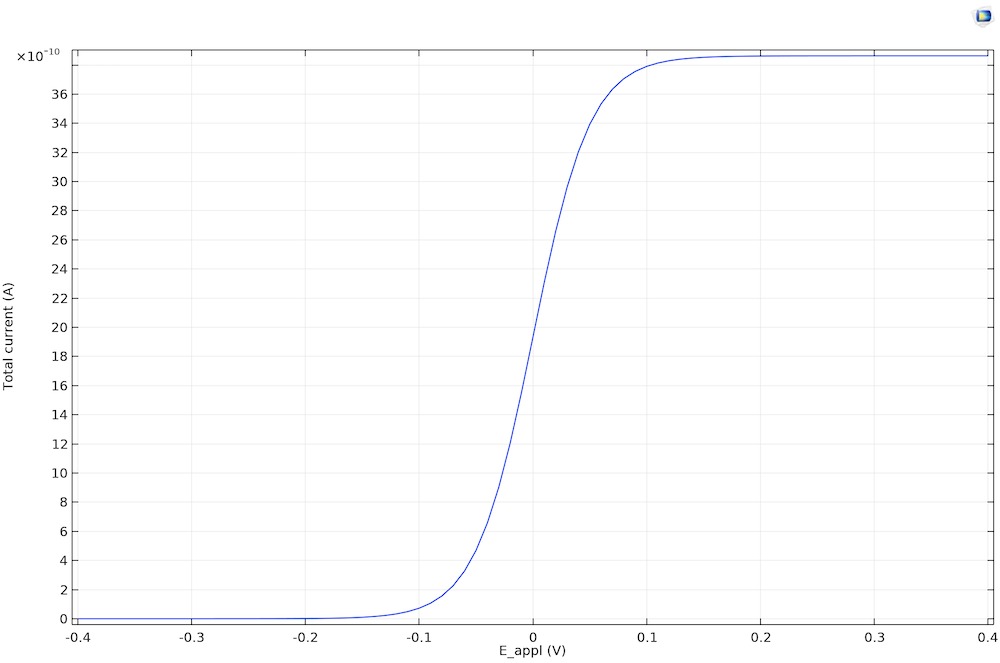
微盤電極上記錄的穩態循環伏安法
由于擴散速率有限,電流密度受到限制。當 E <Eeq. At E< Eeq時,電流密度為 0 (不受限制),在 E< Eeq. At E < Eeq條件下,只有可能發生還原反應,因為電解質中沒有氧化物質,所以什么也不會發生。當氧化反應加速,快到足以消耗電極表面的大量反應物時,電流就會受到 A 物質向工作電極傳遞速率的限制。由于擴散層是平衡的,因此這種受傳遞限制的電流在時間上是恒定的。
因為生成物已擴散到本體溶液中,使用穩態伏安法時,微盤電極不會觀察到負電流。由于在時間尺度上的快速擴散,使本體與電極表面可以快速達到平衡態,在本體電解質中沒有生成物,所以一直是氧化反應過程。
二、電化學阻抗譜
電化學阻抗譜(Electrochemical impedancespectroscopy,簡稱 EIS)是電化學領域廣泛使用的實驗方法,應用于電化學傳感、電池和燃料電池的研究。這項技術的工作原理是,首先在固定電壓下使電池極化,然后施加一個小的附加電壓(偶爾施加電流)來干擾系統。擾動輸入隨時間作時諧振蕩,產生交流電,如下圖所示:
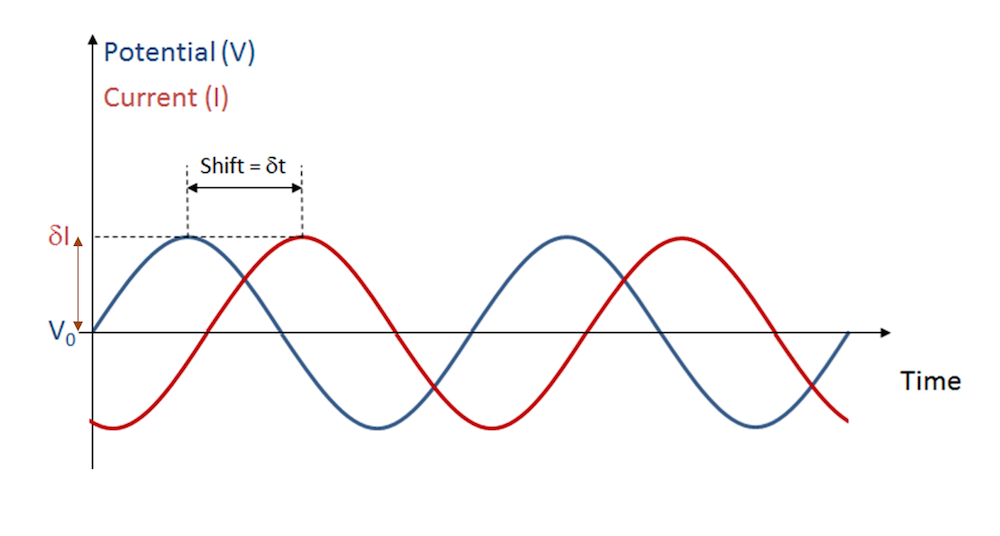
電池電壓的振蕩擾動產生振蕩電流響應
在特定幅度和頻率的外加電壓下,電化學電池產生頻率相同的特定振幅的交流電。在實際系統中,對于其他頻率的分量,響應也可能非常復雜,我們將在下文進行討論。
在 EIS 實驗中,我們通常在 mHz 到 kHz 范圍內改變所施加的擾動的頻率,響應的相對振幅以及輸入信號與輸出信號之間的時移(或相移)隨施加的頻率而變化。
這些因素取決于電化學電池中的物理過程對振蕩激勵的響應速度。不同的頻率能夠區分具有不同時間尺度的不同過程。在較低頻率下,有時間進行的擴散或緩慢的電化學反應,以響應電池的交替極化;在較高頻率下,外加激勵比化學反應更快地改變方向,因此響應主要由雙層充放電的電容決定。
時域響應不是解釋這些頻率相關振幅和相移的最簡潔的方法。因此,我們定義了一個稱為阻抗 的量。像靜態系統中的電阻一樣,阻抗是電壓與電流的比值,但它使用復數的實部和虛部來表示振幅和相位與輸入信號和輸出響應的關系。將阻抗與時域響應聯系起來的數學工具是傅立葉變換,它表示振蕩信號的頻率分量。
為了更全面地解釋簡單情況下的阻抗概念,我們將輸入電壓看作以角頻率(ω)振蕩的余弦波:
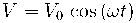
由此可見,響應也是余弦波,但具有相位偏移(φ)。與上圖中的時移相比,相位偏移表示為:
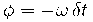
電流的大小及其相位偏移取決于電池的物理和化學性質:
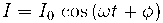
現在,我們通過歐姆定律推導出電阻:
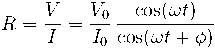
這個量隨時間變化,其頻率與擾動信號的頻率相同。當分子等于零時,這個量值為零;當分母等于零時,值異常。因此,與直流系統中的電阻不同,它不是一個非常有用的量!
相反,根據歐拉定理,我們將時變量表示為復指數的實部,因此:
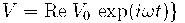
并且
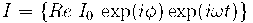
![]()
這些量是復振幅,可以根據原始時域正弦信號的傅立葉變換來理解,它們表示電壓和電流的不同振幅和相位差。由于系統中的所有量都呈正弦振蕩,因此我們通過比較這些復雜的量(而不是時域量)來理解物理效應。為了描述振蕩問題(通常稱為相量理論),我們將電阻的復數量模擬定義為:
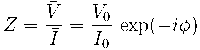
這是系統的阻抗,顧名思義,是我們在電化學阻抗譜中測量的量,它是具有大小和相位的復數量,代表電阻和電容效應。電阻是復數阻抗的實部,與施加的電壓同相,電容是復數阻抗的虛部,與施加的電壓不同相。
EIS 專業人員以頻譜的形式觀察阻抗,通常使用奈奎斯特圖,該圖能夠表現出阻抗虛部與實部的關系,在測量阻抗的每個頻率下都有一個數據點。下圖是一個仿真示例,我們將在下一節中討論具體的建模過程。
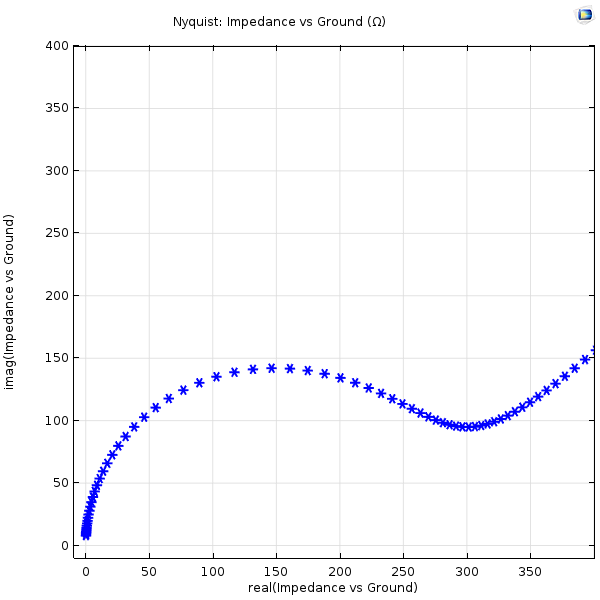
基于電化學阻抗譜實驗的模擬奈奎斯特圖。右上角的點處于低頻率(mHz),左下角的點處于較高頻率(>100 Hz)。
在上圖中,左側的半圓形區域顯示了在快于物理擴散過程的頻率下,雙層電容與電極動力學效應之間的耦合,右側的“擴散尾”對角線顯示較低頻率下的擴散效應。
由于 EIS 實驗可以從一次分析中提取出許多不同物理效應的信息,因此這種實驗非常有用。奈奎斯特圖中的擴散系數、動力學速率常數和特征尺寸等屬性之間存在定量關系。通常,EIS 實驗是通過電阻和電容的“等效電路”來解釋的,該電路產生的頻率相關阻抗與上面奈奎斯特圖中所示的阻抗相似。
當電壓與電流之間存在線性關系時,傅立葉變換中只會出現一個頻率,從而可以大大簡化分析過程。
為了解釋阻抗方面的簡諧波,我們需要電流響應以與輸入電壓相同的頻率振蕩,這意味著系統必須做出線性響應。對于電化學電池來說,我們通常可以通過確保外加電壓比 RT/F 小來實現這一點,RT/F是氣體常數和溫度的乘積與法拉第常數的比值,這就是電化學中特有的“熱電壓”,在常溫下約為 25 mV。較小的電壓變化通常會引起線性響應,而較大的電壓變化會引起明顯的非線性響應。
當然,通過仿真來預測時域電流時,我們隨時可以考慮非線性情況,并用數值方法進行傅立葉變換來研究其對阻抗的影響。實際上,上述阻抗解釋最適合諧波假設。因此,阻抗測量通常以與瞬態技術互補的方式使用,如電流分析法或伏安法,這些技術更適合研究非線性效應或滯后效應。
總結
在電化學領域,許多過程都能進行仿真模擬。通過模擬能幫助優化設計,幫助我們分析和理解各種物理過程,提高科研效率,有助于創造優質科研成果。











